15 理解周期性交易行为
📜 [原文1]
在本节中,我们进行额外的分析,以理解我们记录的周期性交易行为。我们承认,为了确定性地查明周期性交易行为的来源,需要投资者的身份标签,而我们无法获取这些标签。因此,我们进行了七项不同的分析,而不依赖于身份信息,这些分析综合起来表明,交易量中的周期性可能反映了具有重复且定期交易指令的交易算法的行为。
本段是第 5 节的引言,其核心作用是设定本章节的研究目标和方法论基调。作者在这里明确指出,本节的目的是深入探究在前文(第 4 节)中发现的“周期性交易行为”背后的原因。
- 提出研究问题: “理解我们记录的周期性交易行为”。这句话直接点明了本节的核心任务。前面章节已经通过谱分析等方法证明了交易量(特别是成交笔数)在特定频率(如 10 秒、1 分钟、5 分钟)上存在显著的周期性,即交易活动会像波浪一样有规律地起伏。现在的问题是:这种规律性的起伏到底是什么原因造成的?
- 承认研究局限性: “我们承认,为了确定性地查明周期性交易行为的来源,需要投资者的身份标签,而我们无法获取这些标签。” 这是一个非常重要且诚实的表述。最直接、最无可辩驳地找出周期性来源的方法,就是拿到每一笔交易背后的投资者身份信息。例如,如果能看到是A基金、B散户、C高频交易公司下的单,就可以直接统计是不是某个或某类特定投资者在特定时间点集中交易,从而导致了周期性。但这类数据通常是高度机密和受监管的,研究者几乎不可能获取。这为论文的研究设置了一个天然的障碍。
- 提出替代研究方案: “因此,我们进行了七项不同的分析,而不依赖于身份信息”。既然最直接的路径走不通,作者选择了一条“旁敲侧击”、“多方取证”的道路。他们设计了七种不同的间接分析方法。这些方法不依赖于具体的投资者身份,而是通过分析可观测的市场数据(如不同交易量度量、股票特征、策略盈利能力、价格冲击等)来推断周期性的来源。
- 给出核心假设/结论: “这些分析综合起来表明,交易量中的周期性可能反映了具有重复且定期交易指令的交易算法的行为。” 这是本节的中心论点。作者预先声明,通过这七项分析,所有的证据都指向一个共同的解释:这种周期性很可能是由交易算法(Algorithmic Trading)造成的。这些算法被设定为按照固定的时间间隔(“定期”)重复执行交易指令,从而在宏观的交易量数据上留下了周期性的印记。
- 因果与相关的混淆: 本段明确指出,由于缺乏投资者身份数据,所有的分析都是相关性分析,而非因果性分析。读者必须清楚,论文的结论是“周期性与算法交易的特征一致”,而不是“算法交易导致了周期性”。虽然暗示了因果关系,但在学术上保持了严谨。
- “交易算法”的宽泛定义: 这里的“交易算法”是一个广义概念,既包括追求微秒级优势的高频交易(HFT),也包括机构投资者用来拆分大订单以减小市场冲击的执行算法(如 VWAP, TWAP),还包括基于特定信号进行套利的策略算法。论文的结论并未精确区分是哪一种算法,而是泛指所有具有自动化、重复性、定时性特征的交易程序。
- 证据的间接性: 七项分析提供的都是间接证据。每一项单独拿出来可能都有其他解释,但作者的论证逻辑是,当七个独立的证据都指向同一个方向时,这个解释(算法交易驱动)的可能性就变得非常高。这是一种“证据三角测量”(Triangulation)的逻辑。
本段作为第 5 节的开篇,明确了研究目标(解释周期性交易行为的来源)、承认了核心局限(无法获取投资者身份)、提出了替代方案(进行七项不依赖身份的间接分析),并预告了最终的核心论点(周期性很可能源于交易算法的重复性、定时性指令)。
本段的存在是为了给整个第 5 节搭建一个清晰的逻辑框架。它像一个“路标”,告诉读者接下来要看什么(七项分析)、为什么这么做(因为拿不到直接证据),以及最终要得出什么结论(算法交易是可能的解释)。这使得后续复杂的分析内容能够被读者置于一个明确的上下文中,更容易理解其论证目的。
想象一下你是一名侦探,正在调查一桩连环案件。每个案子都在每周三晚上8点准时发生。
- 直接证据: 你拿到了凶手的DNA,直接锁定了嫌疑人。这相当于拿到了投资者的身份标签。
- 间接证据: 你没有DNA。但你发现:
- 案发地点的监控都拍到一个穿着同样雨衣的人。
- 受害者都属于同一家公司的员工。
- 每次案发后,某个特定的网络论坛都会出现一篇相关的匿名帖子。
...(七项证据)
虽然没有一项能直接指认凶手,但所有线索都指向一个有固定作息、熟悉该公司、并混迹于该论坛的人。
这七项分析就像这七条间接线索,共同指向“交易算法”这个“嫌疑人”。
想象一条河流,河水流量通常是平稳变化的。突然,你发现每到整点(比如上午9点、10点、11点),河水的流量都会猛增一下,然后迅速回落,形成规律性的洪峰。你不知道是谁在放水,但你猜测上游可能有一个或多个水坝,它们的闸门被设定为每小时自动开启一次,进行规律性泄洪。这里的“河水流量”就是交易量,“规律性的洪峰”就是周期性交易行为,而那个“自动定时的水坝闸门”就是交易算法。本节就是要通过分析水质、流速、河床变化等七个方面,来证明这个“水坝理论”是靠谱的。
5.1 交易量度量指标、横截面和时间序列的变化
51.1 不同的交易量度量指标
📜 [原文2]
在我们的主要分析中,我们选择成交笔数作为我们的交易量度量指标,而不是成交股数或成交金额。本节表明,周期性交易行为在三种不同的交易量度量指标中都是稳健的。然而,当以成交笔数衡量时,这种行为最强。这与算法交易员驱动这一现象的解释一致,因为他们倾向于通过拆分大额订单来发送小额订单 (O'Hara, Yao, and Ye, 2014, Johnson, Van Ness, and Van Ness, 2017)。
- 回顾主要选择: 作者首先重申,在之前的主体分析(第 4 节)中,他们衡量交易量(Volume)的核心指标是成交笔数(Number of Trades)。交易量可以有多种衡量方式:
- 成交笔数 (Number of Trades): 在一个时间单位内,发生了多少次买卖撮合。例如,1秒内发生了100次交易,成交笔数就是100。
- 成交股数 (Number of Shares): 在一个时间单位内,总共成交了多少股股票。例如,1秒内一笔成交了1000股,另一笔成交了2000股,总成交股数就是3000股。
- 成交金额 (Dollar Volume): 在一个时间单位内,总成交金额是多少。例如,成交了3000股,每股10美元,成交金额就是30000美元。
- 提出第一个证据(稳健性): 本节的第一个发现是,无论用这三种指标中的哪一种来衡量交易量,都能观察到周期性交易行为。这说明周期性这个现象不是偶然的,不是因为作者碰巧选了成交笔数这个指标才出现的。它是一个“稳健”(robust)的现象。
- 提出第二个证据(强度差异): 尽管三种指标都有周期性,但强度不同。“当以成交笔数衡量时,这种行为最强。” 这意味着,如果画出三种交易量时间序列的频谱图,成交笔数在那些特定频率(如10秒、1分钟)上的“峰”会比成交股数和成交金额的“峰”更高、更尖锐。
- 关联到核心论点: 这个“强度差异”是支持“算法交易驱动论”的一个关键证据。为什么呢?作者引用了文献,指出现代算法交易(特别是执行算法)的一个普遍特征是“订单拆分”(Order Splitting)。一个机构投资者想买100万股某支股票,如果一次性下一个100万股的大单,会立刻暴露意图,并对市场价格产生巨大冲击(推高股价),导致自己的买入成本大幅上升。为了隐藏意图并降低交易成本,交易算法会自动将这个100万股的大单拆分成几百甚至几千个小订单(比如每笔只买500股或1000股),在一段时间内分批执行。
- 逻辑推演: 如果是算法交易在特定时间点集中活动,由于订单拆分的存在,我们会观察到:
- 成交笔数会急剧增加(很多小订单被执行)。
- 但每笔交易的平均股数和平均金额会很小。
- 因此,成交股数和成交金额的增幅,相对成交笔数的增幅来说,就不会那么剧烈。
- 这完美地解释了为什么周期性在成交笔数上表现得最强。
- 指标选择的合理性: 为何一开始就选成交笔数?因为成交笔数更能代表“交易决策”的频率。一笔交易代表一次买方和卖方的意愿撮合。而成交股数或金额则可能受到单笔异常大额交易的严重影响,产生噪声。
- 对“强”的量化: 这里的“强”是通过频谱分析中的强度系数或频率方差比(fVR)来量化的,这些指标越高,代表该频率的周期性越强。
本段通过比较成交笔数、成交股数、成交金额这三种交易量度量指标,发现周期性在三者中都存在,但在成交笔数中最为显著。这一发现与算法交易倾向于拆分大额订单为多个小额订单执行的特征高度吻合,从而为“周期性由算法交易驱动”的论点提供了第一项有力证据。
本段的目的是通过分析不同交易量度量指标的差异,来验证和加强论文的核心假设。它不仅证明了现象的稳健性,更重要的是,通过分析强度差异,找到了一个与算法交易特定行为(订单拆分)相匹配的“指纹”,使论证更有说服力。这是七项分析中的第一项,为整个论证过程奠定了基础。
想象一个超市收银台。我们可以用三个指标衡量它的繁忙程度:
- 结账次数(相当于成交笔数)
- 卖出商品总件数(相当于成交股数)
- 总销售额(相当于成交金额)
假设超市搞了一个活动,每个整点开始的前10秒,用自助收银机结账可以打折。一群精明的顾客(算法交易员)发现,为了快速结账享受折扣,最好是每次只结账一件商品(拆分订单)。于是在每个整点,我们看到:
- 结账次数飙升,因为很多人都在快速地一次只刷一件商品。
- 卖出商品总件数和总销售额也增加了,但增幅远不如结账次数那么夸张,因为每次结账的商品和金额都很小。
这个场景就解释了为什么周期性在“结账次数”(成交笔数)上最强。
想象你在听一段音乐。这段音乐有一个固定的鼓点节奏,比如每秒敲一次鼓。
- 成交笔数: 就像是你直接听到的鼓声次数,每秒一次,节奏非常清晰、强烈。
- 成交股数/金额: 想象每次敲鼓的同时,还会伴随一个随机响度的钹声(可能很响,也可能很轻)。你听到的总音量(鼓声+钹声)虽然也有每秒一次的节奏感,但由于钹声响度随机,这个节奏感就被削弱和模糊了,不如单纯的鼓声那么“强”。这里的“随机响度的钹声”就代表了每笔交易股数/金额的随机性。
📜 [原文3]
我们对成交股数和成交金额进行了与第 4 节并行的分析,发现这些替代定义的交易量中的周期性与第 4 节中的结果一致。附录 G 中的图 A.8 - A.11 详细总结了这些结果。这些发现也与 Broussard and Nikiforov (2014) 的结果一致,他们研究了成交股数和成交笔数中的成交量。
- 重复分析过程: 作者说明,他们把之前在第 4 节里对成交笔数做的全套分析流程(包括数据处理、谱分解、计算强度系数和 fVR 等),又原封不动地在成交股数和成交金额这两个指标上重新做了一遍。这被称为“并行分析”(parallel analysis),是保证结果可比性的标准做法。
- 结果一致性: 分析发现,用成交股数和成交金额得到的结果,在性质上与用成交笔数得到的结果是“一致的”。“一致”在这里意味着:
- 同样在那些特定频率(如10秒、1分钟等)上观察到了周期性。
- 周期性的强度排序可能也类似(例如,1分钟的周期性强于2分钟的)。
- 这再次确认了周期性现象的稳健性。
- 引用附录证据: 为了不让主文过于臃肿,详细的图表结果被放在了论文的附录(Appendix G)中。图 A.8 到 A.11 应该是展示了成交股数和成交金额的频谱分析结果,读者可以去附录查看原始证据。这是学术写作的常规做法,主文只呈现关键结论,支撑性的细节放在附录。
- 与现有文献的联系: 作者还将自己的发现与 Broussard and Nikiforov (2014) 的研究进行了比较。该文献也研究了成交股数和成交笔数,并且得出了类似的结论。引用这篇文献的作用有二:
- 增加可信度: 表明作者的发现不是孤立的,与该领域其他研究者的观察相符,这大大增强了结果的可靠性。
- 体现学术传承: 表明作者了解该领域的研究现状,并将自己的工作建立在已有知识的基础上。
- “一致”不等于“相同”: “一致”指的是定性上相同(都有周期性),但定量上(周期性的强度)是不同的,这正是下一段要深入探讨的关键点。
- 查阅附录的重要性: 对于严谨的读者或审稿人来说,必须去查看附录 G 中的图表,才能完全相信作者的陈述。主文中的一句话陈述是结论,附录中的图表是证据。
本段通过重做分析和引用附录图表,证实了周期性在成交股数和成交金额中也普遍存在,与使用成交笔数时的发现定性一致。同时,通过引用先前的研究,进一步巩固了这一发现的可靠性。
本段的目的是提供证据支持,证明周期性的发现是稳健的,不依赖于特定的交易量指标。同时,通过与现有文献对比,将本研究置于更广阔的学术背景中,增加其科学性和可信度。这是构建论证链条中“确认现象普遍性”的一步。
继续用超市收银台的例子。研究员A只统计了“结账次数”,发现每个整点都有高峰。现在,研究员B和C分别统计了“卖出商品总件数”和“总销售额”,他们也发现每个整点都有高峰。这就说明,“整点高峰”这个现象是真实存在的,不是因为研究员A碰巧选了个奇怪的统计方法。而且,他们还发现,隔壁镇的另一位研究员D在2014年研究另一家超市时,也发现了类似的现象。这让大家对“整点高峰”这个结论更加深信不疑。
医生给病人做检查。
- 第4节的分析: 医生用听诊器(成交笔数)听心脏,听到了规律性的杂音(周期性)。
- 本段的并行分析: 为了确认,医生又用了心电图(成交股数)和超声心动图(成交金额)来检查。结果发现,这两种检查也都显示心脏有同样的规律性异常。
- 引用文献: 医生还查了医学文献,发现2014年的一篇论文里描述过非常相似的病例。
- 结论: 医生现在非常确定,这个病人的心脏确实存在规律性的问题,需要进一步探究原因。
📜 [原文4]
然而,我们也观察到成交股数和成交金额中的周期性略弱于成交笔数中的周期性。为了理解是什么驱动了这些度量指标之间的差异,我们观察以下关系:
因此,我们遵循与第 4 节相同的方法,通过分别用每笔交易平均股数和每笔交易平均金额替换成交笔数来估计强度系数。图 5 显示了使用每笔交易平均股数时的前三个频率。与图 3 形成鲜明对比的是,极少数股票在选定频率上显示出周期性。
- 引出核心问题: 本段开始深入探究前述的“强度差异”。作者明确指出成交股数和成交金额的周期性比成交笔数的“略弱”(slightly weaker)。现在的问题是:为什么会变弱?是什么因素“稀释”了周期性?
- 建立数学分解关系: 为了回答这个问题,作者引入了两个近似的恒等式(公式8)。这两个公式是将成交股数和成交金额进行分解:
- 成交股数 ≈ 成交笔数 × 每笔交易平均股数
- 成交金额 ≈ 成交笔数 × 每笔交易平均金额
- 提出研究假设: 基于这个分解,逻辑上的推断是:如果成交笔数是强周期性的,而成交股数的周期性较弱,那么问题一定出在“每笔交易平均股数”这个因子上。这个因子很可能是非周期性的,或者说它的波动是随机的、充满噪声的。当一个强周期性信号(成交笔数)与一个随机噪声信号(每笔交易平均股数)相乘时,得到的结果(成交股数)的周期性就会被“稀释”和削弱。
- 设计实验验证假设: 为了验证这个假设,作者设计了一个新的分析:直接对“每笔交易平均股数”和“每笔交易平均金额”这两个时间序列本身进行频谱分析。他们采用了与第 4 节完全相同的方法,来计算这两个新指标的强度系数。
- 呈现结果: 图 5 展示了对“每笔交易平均股数”进行分析的结果。这个图的作用是与之前的图 3(基于成交笔数的分析结果)进行对比。
- 图 3 的情况: 大量的股票在特定频率(如10秒、1分钟)上表现出最强的周期性,所以柱子很高。
- 图 5 的情况: “与图 3 形成鲜明对比的是,极少数股票在选定频率上显示出周期性。” 这意味着图 5 的柱子会非常矮,说明几乎没有股票在这些频率上表现出显著的周期性。
- 得出结论: 这个对比结果强有力地证明了假设:每笔交易平均股数这个变量本身基本上是“非周期性”的(或者说是“非周期的”)。
- 公式 (8):
- 成交笔数 (Number of Trades): 在一个时间单位内(例如1秒),交易发生的次数。符号:$N_{trades}$。
- 每笔交易平均股数 (Average Shares per Trade): 在该时间单位内,总成交股数除以总成交笔数。符号:$\bar{S}$。
- 成交股数 (Total Shares Traded): 在该时间单位内,成交的总股数。符号:$S_{total}$。
- 每笔交易平均金额 (Average Dollar Volume per Trade): 在该时间单位内,总成交金额除以总成交笔数。符号:$\bar{V}$。
- 成交金额 (Total Dollar Volume): 在该时间单位内,成交的总金额。符号:$V_{total}$。
- 推导:
- 定义上,$\bar{S} = S_{total} / N_{trades}$。所以,$N_{trades} \times \bar{S} = S_{total}$。这里用约等号 $\approx$ 是因为实际计算中可能存在微小的数据处理差异,但基本上是恒等关系。
- 同理,$\bar{V} = V_{total} / N_{trades}$。所以,$N_{trades} \times \bar{V} = V_{total}$。
- 示例1: 算法交易主导的场景
- 时间:上午10:00:00 - 10:00:01 (1秒内)
- 成交笔数: 发生了 200 笔交易。
- 成交股数: 总共成交了 40,000 股。
- 每笔交易平均股数: 40,000 股 / 200 笔 = 200 股/笔。
- 验证:200 笔 × 200 股/笔 = 40,000 股。
- 示例2: 非算法交易主导的场景
- 时间:上午10:01:00 - 10:01:01 (1秒内)
- 成交笔数: 发生了 5 笔交易。
- 成交股数: 总共成交了 20,000 股。
- 每笔交易平均股数: 20,000 股 / 5 笔 = 4,000 股/笔。
- 验证:5 笔 × 4,000 股/笔 = 20,000 股。
这个对比清晰地显示了,在算法交易主导的时间点(示例1),成交笔数高而每笔平均股数低。
- 混淆平均值和单笔值: “每笔交易平均股数”是一个时间窗口内的平均值,不代表该窗口内每一笔交易都是这个股数。窗口内可能有一笔10000股的交易和很多笔100股的交易。
- 噪声的来源: 每笔交易平均股数之所以像噪声,是因为它受到交易者类型的异质性影响。同一秒内,既可能有算法的小单,也可能有散户的中单,还可能有机构的大单。这些混合在一起,使得平均股数变得非常不规律。
本段通过将成交股数/金额分解为成交笔数和每笔平均股数/金额的乘积,并单独分析每笔平均股数的周期性,发现后者几乎没有周期性。这有力地证明了,成交股数/金额的周期性被削弱,是因为强周期性的成交笔数乘以了一个近似于随机噪声的每笔平均股数/金额因子。
本段的目的是深入解释“为什么周期性在成交笔数中更强”这个关键观察。通过这个分解和验证,作者将周期性的来源更精确地定位到了“交易发生的频率”(成交笔数)上,而排除了“交易规模的规律性变化”(每笔平均股数)。这使得“算法交易的订单拆分”这一解释变得更加坚实和具体。
你有一支信号非常稳定、每秒闪烁一次的LED灯(强周期性的成交笔数)。现在你用一张半透明的、厚度不均的毛玻璃片挡在LED前面(充满噪声的每笔平均股数)。
你透过毛玻璃看到的光(成交股数),虽然仍然能感觉到它在每秒闪烁,但由于玻璃厚度不均导致光线被随机散射和吸收,闪烁的明暗对比变弱了,节奏感也不如直接看LED那么清晰了。
本段的分析,就相当于把毛玻璃片拿开,单独去检查这张玻璃片本身,发现它上面没有任何规律性的图案,完全是随机的。这就证明了信号变弱是毛玻璃片(每笔平均股数)的错。
想象一个合唱团在唱歌。
- 成交笔数: 就像是合唱团里所有人都严格按照节拍器,在每个节拍点上准确地发出一个声音。这个节拍感非常强。
- 每笔平均股数: 就像是每个唱歌的人在发声时,被允许自由决定自己用多大的音量来唱(音量随机)。
- 成交股数: 听众听到的总音量。虽然总音量也随着节拍起伏,但因为每个人的音量随机,导致整体的节奏感被削弱了,不如单纯听节拍器那么清晰。
本段的分析就是把每个人的音量变化单独录下来分析,发现它毫无规律可言,从而证明总音量节奏感减弱是“随机音量”这个因素造成的。
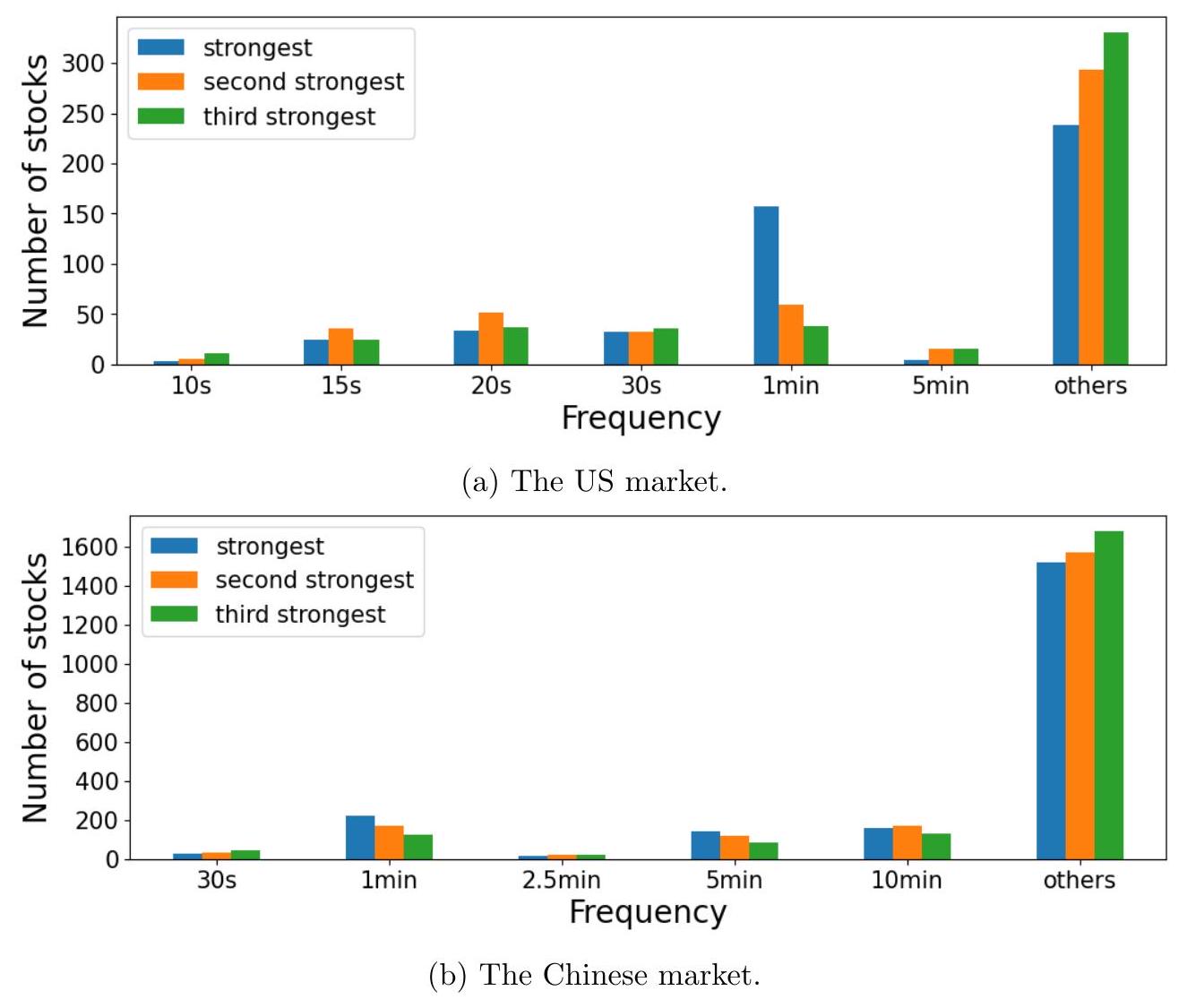
📜 [原文5]
图 5:2019-2021 年间,当使用每笔交易平均股数时,各频率作为所有股票中估计强度系数最强的前三个频率的出现次数。
- 图表标题解读:
- 时间范围: 2019-2021年,与主分析的样本期一致。
- 分析指标: “每笔交易平均股数 (Average Shares per Trade)”。这是本分析的核心,与之前分析成交笔数形成对比。
- 分析方法: 对每一支股票,首先计算其“每笔交易平均股数”的时间序列。然后对这个时间序列做谱分析,得到在不同频率下的强度系数。找出这支股票强度系数最高的三个频率。
- 纵轴 (Y-axis): “出现次数 (Counts)”。这个计数是指,在所有被分析的股票中,有多少支股票的最强三个频率中包含了X轴对应的那个频率。
- 横轴 (X-axis): “频率 (Frequency)”。列出了一系列备选的频率,如 10s (秒), 15s, 20s, 30s, 1m (分钟), 5m, 10m 等。
- 图表内容分析:
- 从图上看,所有频率对应的柱子都非常非常矮,几乎贴近于0。最高的柱子(例如10分钟和1分钟)的计数值也远小于图3中相应的数值。
- 这意味着,对于绝大多数股票来说,它们的“每笔交易平均股数”这个指标,其能量(方差)并没有集中在任何一个特定的周期性频率上。它的频谱更像是一条平坦的线,没有明显的“峰”。
- 即使某个频率(比如10分钟)的柱子比其他的高一点,其绝对值也非常小,说明只有极少数的股票在这个频率上表现出最强的“周期性”,而这种“周期性”本身可能也只是噪音导致的假象。
- 与图3的对比:
- 此图的关键在于和图3(基于成交笔数的同一分析)形成“鲜明对比”。
- 图3 中,10秒、1分钟等频率的柱子非常高,说明对于成百上千支股票来说,成交笔数的最强周期性就集中在这些频率上。
- 图5 中,所有柱子都接近于零,说明“每笔交易平均股数”这个指标缺乏共同的、显著的周期性。
- 计数的含义: 这个图显示的不是周期性的平均强度,而是某个频率成为“最强频率之一”的股票数量。即使一个频率的强度很弱,但只要它比其他频率的强度稍微高一点点,也会被计数。因此,图5中柱子如此之矮,更加凸显了每笔交易平均股数中周期性的缺失。
- “无周期性”的含义: 这里的“无周期性”是指在研究者关心的这些特定高频频率上没有系统性的周期性。它不排除在其他更长(如日、周、月)或更短(毫秒级)的时间尺度上可能存在某种模式。
图5通过可视化地展示对“每笔交易平均股数”进行谱分析的结果,清晰地表明这个指标在整个市场范围内普遍缺乏在特定频率上的周期性。它为“成交笔数的周期性被每笔平均股数的随机性所稀释”这一论点提供了强有力的图形证据。
该图的目的是为了提供一个与图3直接、鲜明对比的视觉证据。文字可以说“形成鲜明对比”,但一张图能够让读者瞬间理解这个对比有多么“鲜明”。它将抽象的“周期性缺失”概念转化为了直观的、接近于零的柱状图,极大地增强了论证的说服力。
想象一个班级的学生在进行一场才艺表演投票。
- 图3 (成交笔数): 老师问:“你最喜欢的三个节目是哪个?” 结果,几乎所有学生都投了1号、5号和8号节目。所以在统计图上,1号、5号、8号的柱子特别高。这说明大家的偏好非常集中。
- 图5 (每笔平均股数): 老师换了个问题:“你觉得哪个节目的服装最好看?” 结果学生们的答案五花八门,A同学说2号,B同学说7号,C同学说4号……没有任何几个节目获得集中的票数。在统计图上,所有节目的柱子都差不多高,而且都很矮。这说明大家在“服装”这个维度上没有共同的偏好。
你有一堆混杂着各种沙砾的铁屑。
- 图3 (成交笔数): 你用一块强力磁铁(谱分析)去吸这堆混合物。结果,大量的铁屑(周期性成分)被吸附到了磁铁的N极和S极(特定频率)。你画一张图,显示N极和S极吸附的铁屑数量,会看到两个非常高的柱子。
- 图5 (每笔平均股数): 现在你把铁屑都拿走,只剩下一堆沙砾(每笔平均股数的随机性)。你再用同样的磁铁去吸,结果什么也吸不上来。你再画一张图,所有位置的柱子高度都基本是0。
这张图就直观地告诉你,你分析的“每笔平均股数”这堆东西里,根本不含“铁屑”(周期性)。
📜 [原文6]
此外,图 6 显示了每笔交易平均股数的 fVRs。与图 4 相比,对于大多数股票,fVRs 在所有频率上都更接近 0.2% 的基准水平,这意味着该指标中周期性的证据非常微弱。[^8]
[^8]:
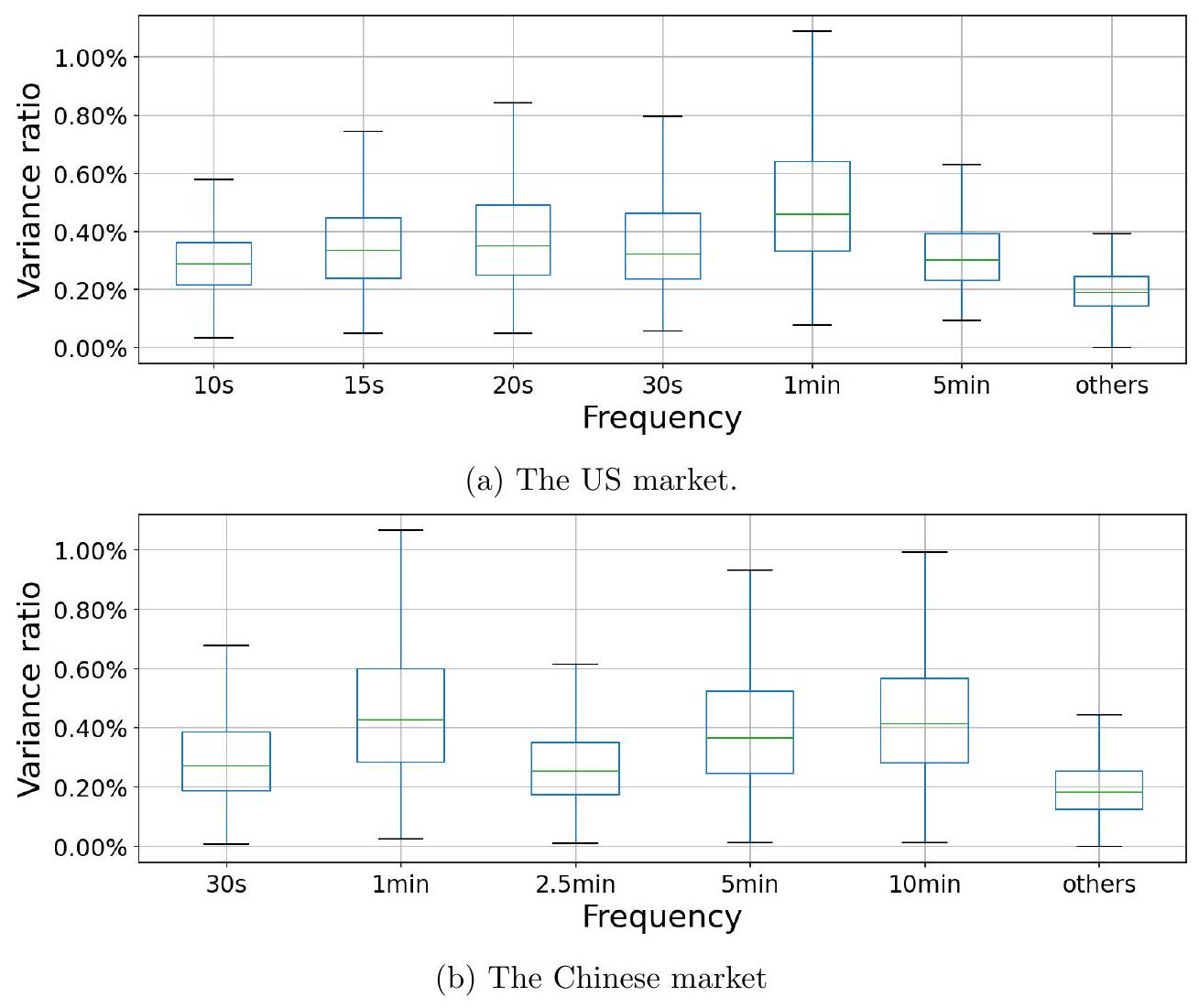
图 6:使用每笔交易平均股数时频率方差比 (fVR) 的箱线图。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为我们在模型中包含了 $n=500$ 个周期分量。
- 引入新证据 (fVRs): 除了图 5 的强度系数计数,作者又提供了另一项证据:频率方差比 (Frequency Variance Ratios, fVRs)。fVR 是一个衡量特定频率周期性强度的更标准化的指标。它的值表示由该频率的周期分量所解释的交易量总方差的百分比。
- fVR 的基准水平: 如果一个时间序列完全是随机的(白噪声),没有任何周期性,那么它的总方差会均匀地分布在所有频率上。论文的模型中包含了 $n=500$ 个频率分量。因此,在完全没有周期性的情况下,每个频率分量应该解释总方差的 $1/500$,即 $0.2\%$。这个 $0.2\%$ 就是一个“基准水平”(benchmark level)或“零假设水平”。如果某个频率的 fVR 显著高于 $0.2\%$,我们就说在这个频率上存在周期性。
- 解读图 6: 图 6 是一个箱线图 (box plot),它展示了在使用“每笔交易平均股数”作为分析对象时,在不同频率下,所有股票的 fVR 值的分布情况。
- 箱线图的每个“箱子”代表了所有股票 fVR 值的中间 50%(从25百分位到75百分位)。
- 箱子中间的线是中位数。
- 上下延伸的“胡须”表示了数据的范围(剔除异常值后)。
- 图中的虚线或基准线应该就画在 $y=0.2\%$ 的位置。
- 分析图 6 的结果: “对于大多数股票,fVRs 在所有频率上都更接近 0.2% 的基准水平”。这意味着:
- 在图 6 中,几乎所有频率的箱线图,其整个箱体和胡须都紧紧地围绕在 $0.2\%$ 这条基准线附近。
- 中位数线几乎就贴在 $0.2\%$ 上。
- 这表明,对于市场上绝大多数股票,“每笔交易平均股数”这个指标在任何一个被测频率上的周期性强度都和随机噪声差不多。
- 与图 4 的对比: 这个结论是与图 4(基于成交笔数的 fVR 分析)进行对比得出的。在图 4 中,10秒、1分钟等频率的箱线图会显著地高于 $0.2\%$ 的基准线,甚至中位数就能达到百分之几,说明成交笔数中存在非常强的周期性。
- 最终结论: 图 6 的结果进一步证实了“该指标中周期性的证据非常微弱”。
- 示例1: 强周期性 (类似图4中成交笔数的情况)
- 股票A,在频率为 1分钟 时的 fVR 计算出来是 5.0%。
- 由于 $5.0\% >> 0.2\%$,我们得出结论,股票A的成交笔数在1分钟频率上具有非常强的周期性。它解释了成交笔数总波动的5%。
- 示例2: 弱/无周期性 (类似图6中每笔平均股数的情况)
- 股票B,在频率为 1分钟 时,对其“每笔交易平均股数”计算出的 fVR 是 0.25%。
- 由于 $0.25\%$ 非常接近基准水平 $0.2\%$,我们认为这点微小的超出很可能是由随机波动造成的,因此结论是股票B的“每笔交易平均股数”在1分钟频率上没有显著的周期性。
- 对于市场上大量的股票,它们在各个频率上的 fVR 值都像股票B这样,紧紧围绕在0.2%附近,从而构成了图6的箱线图。
- fVR 不是绝对强度: fVR 是相对强度,即某个频率解释的方差占 总方差 的比例。如果一个序列本身波动很小(总方差小),即使某个频率的 fVR 很高,其绝对的周期波动幅度也可能不大。
- 模型依赖性: $0.2\%$ 这个基准值是依赖于模型中频率分量总数 $n=500$ 的。如果模型用了 $n=1000$ 个频率,那么基准就变成了 $0.1\%$。这是一个需要注意的模型参数。
本段使用频率方差比 (fVR) 这一更标准化的指标,通过图6的箱线图展示了“每笔交易平均股数”的周期性强度分布。结果显示,在所有被测频率上,其 fVR 值都紧密围绕在理论上的“无周期性”基准水平(0.2%)附近,从而从另一个角度强有力地证明了该指标缺乏周期性。
本段和图6的存在,是为了用一个比“强度系数”更规范、更具统计意义的指标(fVR)来巩固和验证图5的结论。在学术论证中,从多个不同但相关的角度(这里是强度系数计数和 fVR 分布)得出一致的结论,可以大大增强论证的稳健性和说服力。
你是一个公司的CEO,想知道哪个部门对公司的总利润贡献最大。公司总利润是1000万。
- fVR的含义: 每个部门的利润占公司总利润的百分比。
- 基准水平: 假设公司有500个部门($n=500$),如果所有部门贡献均等(完全没重点),那么每个部门的贡献应该是 $1/500 = 0.2\%$。
- 图4 (成交笔数) 的情况: 你发现“销售A部”的利润是50万,占总利润的 $50/1000 = 5\%$。这个 $5\%$ 远大于基准的 $0.2\%$,说明“销售A部”是公司的核心利润来源(强周期性)。
- 图6 (每笔平均股数) 的情况: 你去分析另一个指标,比如“各部门的平均员工年龄”。你计算每个部门对“公司总平均年龄”的贡献(这有点绕,但只是类比),发现每个部门的贡献率都差不多是 $0.2\%$。这意味着,在“员工年龄”这个维度上,没有哪个部门是特别突出或异常的(无周期性)。
你有一杯浑浊的池塘水,你想分析里面有什么成分。
- 总方差: 水的浑浊程度。
- 频谱分析: 你用一个离心机把水里的物质按照重量分层。
- fVR: 每一层的物质占总物质重量的百分比。
- 基准水平 (0.2%): 如果水里是均匀的泥沙,离心后每层的重量都差不多。
- 图4 (成交笔数) 的结果: 离心后,你发现有一层特别厚重,占了总重量的10%。你断定水里有大量的某种特定物质(比如铁砂),这就是周期性。
- 图6 (每笔平均股数) 的结果: 你拿另一杯水(代表每笔平均股数这个指标),离心后发现每一层都薄薄的,重量几乎完全一样。你断定这杯水里没有那种特别的“铁砂”,它只是均匀的泥水(随机噪声)。
📜 [原文7]
总之,这些结果提供了令人信服的证据,表明交易活动中的周期性来自于成交笔数,而不是每笔交易平均股数或每笔交易平均金额。这也与观察到的成交笔数的周期性最强的事实相一致,相比于成交股数或成交金额(见附录 G 中的图 A.8 - A.11)。后两种度量指标中仍然存在周期性的原因是,它们可以表示为周期项与另一个非周期项的乘积,如等式 (8) 所示。但非周期项只是增加了噪声。
- 总结核心发现: “总之”(In summary)表明这是一个小结。作者将前面的分析(图5、图6)汇总成一个核心结论:“交易活动中的周期性来自于成交笔数”。“来自于”这个词非常关键,它指出了周期性的根本源头。周期性的DNA编码在“交易发生的频率”里,而不是“交易的平均规模”里。
- 解释强度差异: 这段话再次回到了最初的观察——为什么成交笔数的周期性最强?现在可以给出完整解释了。
- 成交笔数 = 纯粹的周期性信号 (Periodical Term)。
- 每笔交易平均股数 = 近似随机的非周期性信号 (Aperiodical Term / Noise)。
- 根据公式 (8),成交股数 ≈ 成交笔数 × 每笔交易平均股数。
- 所以,成交股数 ≈ 周期性信号 × 随机噪声。
- 一个纯净的周期性信号乘以一个随机噪声后,得到的信号虽然仍然保留了周期性的特征,但其信噪比会降低,周期性的“强度”会被削弱。这就完美解释了为什么成交股数和成交金额的周期性比成交笔数弱。
- 对噪声的比喻: “但非周期项只是增加了噪声。” (But the aperiodical term just adds noise.) 这句话用一个非常直观的词“噪声”(noise)来描述每笔交易平均股数/金额的作用。它不贡献周期性,反而起到干扰和模糊周期性的作用。
- 引用附录证据: 再次引用附录G的图A.8-A.11,提醒读者那里有关于成交股数和成交金额周期性强度的直接证据,可以直观地看到它们的周期性确实比成交笔数要弱。
- “来自于”不等于“唯一”: 说周期性“来自于”成交笔数,是在当前分析框架下的结论。这不排除可能存在极其微弱的、来自于每笔平均股数的周期性,但它太弱了,以至于可以忽略不计,被当做噪声。科学语言通常是相对的。
- 乘积的频谱: 两个信号时域相乘,其结果的频谱是两个信号频谱的卷积。一个尖峰(周期性的频谱)和一个平坦的谱(噪声的频谱)进行卷积,结果是一个被展宽和拉低的“钝峰”,这在数学上精确描述了周期性“变弱”的过程。
本段对5.1.1节的分析进行了总结,明确指出交易量的周期性根源于成交笔数的周期性,而成交股数和成交金额的周期性较弱,是因为强周期性的成交笔数乘以了作为噪声来源的、非周期性的每笔交易平均股数/金额。
本段的目的是将前面分散的证据(图5、图6、公式8)整合起来,形成一个完整且自洽的逻辑闭环,为“为什么不同交易量指标周期性强度不同”这个问题给出一个清晰、有力的最终答案。这是完成第一项间接证据论证的收尾工作。
你正在听一个广播电台,它正在播放一段节拍清晰的音乐(成交笔数的周期性)。
- 成交笔数: 纯净的音乐信号。
- 每笔平均股数: 广播传输过程中产生的“沙沙”的静电噪音(非周期性项)。
- 成交股数: 你最终从收音机里听到的、混杂了噪音的音乐。
你仍然能听到音乐的旋律和节拍,但“沙沙”声让音乐听起来不那么清晰、纯粹了。本段的结论就是:我们听到的带噪音的音乐,其音乐性完全来自于原始的纯净音乐,而“沙沙”声只是干扰。
你有一张非常清晰的照片,上面是一个黑白相间的、规律的条纹图案(成交笔数的周期性)。
- 成交笔数: 原始的高清条纹照片。
- 每笔平均股数: 你手机屏幕上的一层油腻的、随机分布的指纹(非周期性项/噪声)。
- 成交股数: 你通过这个油腻的手机屏幕看到的条纹图案。
你仍然能看出这是一个条纹图案,但因为指纹的干扰,图案的边界变得模糊,黑白对比度也下降了。本段的结论是:你看到的模糊图案,其“条纹”性质完全来自于原始照片,屏幕上的指纹只起到了把照片弄脏的作用。
📜 [原文8]
算法交易和高频交易中的一种常见做法是将大额订单拆分为较小的订单 (O'Hara, Yao, and Ye, 2014, Johnson, Van Ness, and Van Ness, 2017)。周期性在成交笔数中最强的事实表明,它们可能反映了采用算法交易和算法执行的投资者的行为。
- 重申行业实践: 作者再次强调算法交易(Algorithmic Trading, AT)和高频交易(High-Frequency Trading, HFT)的一个核心策略——“订单拆分”(Order Splitting)。一个大的买卖意图(比如买100万股)会被程序自动拆解成许多笔小额订单,分批在市场上执行。
- 连接证据与结论: 这是本小节(5.1.1)的最终结论句。它将本节的核心实证发现与论文的核心论点直接联系起来。
- 核心实证发现: “周期性在成交笔数中最强”。我们通过分解交易量,证明了周期性的源头是交易发生的次数,而不是每次交易的平均规模。
- 核心论点: “它们可能反映了采用算法交易和算法执行的投资者的行为”。
- 逻辑桥梁: 算法交易的订单拆分行为,天然就会导致在特定时间点产生大量的交易“笔数”,而每笔的规模相对较小。这与我们的实证发现完美匹配。如果周期性是由非算法交易者(如传统散户或机构)驱动的,他们往往倾向于下达数量较少但金额较大的订单,那么我们应该观察到成交股数或成交金额的周期性更强,但这与事实相悖。
- 精确用词:
- “算法交易” (Algorithmic Trading): 一个广义词,泛指使用计算机程序决定交易的各个方面(时间、价格、数量等)。
- “算法执行” (Algorithmic Execution): 算法交易的一个子集,特指以最优方式执行一个已经决定好的大额订单的算法,例如前面提到的VWAP、TWAP等,它们的核心任务就是拆分订单以降低市场冲击。
- “可能反映了” (may reflect): 再次体现了学术的严谨性。因为是间接证据,所以不用“证明了”(prove)或“导致了”(cause),而是用更温和的“可能反映了”。
- 订单拆分不是算法交易的唯一特征: 算法交易还包括很多其他策略(如做市、套利等),但订单拆分是其中与“成交笔数”这个指标关系最直接、最显著的特征。
- 其他可能性: 尽管匹配度很高,但理论上可能存在其他未知的市场行为也能导致“高成交笔数、低平均规模”的现象。但基于现有金融市场微观结构的知识,算法交易是最合乎逻辑、也是最普遍的解释。
本段是5.1.1节的点睛之笔。它明确地将“周期性在成交笔数中最强”这一关键实证发现,归因于算法交易和高频交易中普遍存在的“订单拆分”行为,从而为“周期性源于算法交易”的核心论点提供了第一项坚实、具体的证据。
本段的目的是将前面所有的技术性分析(公式分解、图5、图6)的结论,清晰地转化为主旨服务的论据。它像一个“翻译官”,把复杂的数理统计结果“翻译”成了与金融市场实践相关的、易于理解的逻辑论证,完成了从“是什么”到“为什么”的飞跃。
一位警官在分析一起银行抢劫案的监控录像。
- 证据(实证发现): 警官发现,在抢劫发生的那一分钟里,有超过100个不同的人进出银行大门(成交笔数高),但每个人手里都只拿了一小袋硬币(每笔平均规模小)。
- 行业知识(文献): 警官知道,现代有组织犯罪集团有一种“蚂蚁搬家式”的作案手法,他们会让大量成员同时行动,每人只拿走少量财物,以避免引起注意。
- 结论(本段论证): 警官推断,这次抢劫“可能反映了”一个有组织犯罪集团的行为,而不是一个单独的劫匪冲进去抢了一大袋钱。这个推断就和本段的逻辑完全一样。
想象你在观察一个蜂巢。
- 实证发现: 你注意到,每到中午12点整,都会有成千上万只蜜蜂飞出蜂巢(成交笔数高),但你用高速摄像机拍下来分析,发现每只飞出去的蜜蜂嘴里只衔了一小滴花蜜(每笔平均规模小)。
- 生物学知识: 你知道,某些种类的蜜蜂演化出了一种集体采蜜的策略,蜂后会在特定时间发出信号,所有工蜂立刻出动,每只采集少量花蜜后迅速返回,以最高效率利用短暂的开花期。
- 结论: 你推断,中午12点的蜜蜂倾巢出动现象,“反映了”这个蜂群的集体采蜜行为。这个逻辑就是将宏观观察(高成交笔数)与微观行为(订单拆分/单次少量采蜜)联系起来的过程。
51.2 与股票特征的相关性
📜 [原文9]
在本节中,我们展示了具有更高水平算法交易的股票和交易日往往在交易量中具有更强的周期性。
- 宣告本节目标: 这句话是 5.1.2 节的开场白和核心论点。它预告了本节即将进行的分析内容和预期结论。
- 核心论点拆解:
- 分析对象: “具有更高水平算法交易的股票和交易日”。这意味着分析将不再是泛泛地看整个市场,而是要区分“算法交易活跃”和“算法交易不活跃”的场景。
- 如何衡量“更高水平的算法交易”: 论文接下来会引入一系列公认的“算法交易代理指标”(proxies for algorithmic trading)。因为我们无法直接观测算法交易的量,所以只能通过一些可观测的、与算法交易高度相关的特征来间接衡量。
- 预期发现: “往往在交易量中具有更强的周期性”。作者预期会发现一个正相关关系:算法交易越活跃的股票或交易日,其交易量的周期性就越强。
- 论证逻辑: 这个论证非常直接。如果周期性确实是由算法交易引起的,那么在算法交易更密集的地方,周期性的信号自然应该更强。反之,如果在一个几乎没有算法交易的股票上仍然观察到很强的周期性,那么“算法交易驱动论”就会受到挑战。
- 代理指标的局限性: 所有的代理指标都只是近似。例如,后面会用到的“消息数量”(message count)可以代表算法交易活跃度,但它也可能因为公司发布重大新闻而飙升。因此,使用多个代理指标并进行综合判断是至关重要的。
- 相关不等于因果: 本节的分析将是回归分析,旨在建立相关性。即使发现算法交易代理指标与周期性强度显著正相关,也不能在统计上断言前者“导致”了后者。但它会为因果关系提供强有力的暗示。
本段简洁地阐明了 5.1.2 节的分析任务:通过检验算法交易活跃度与周期性强度之间的相关性,来为“周期性由算法交易驱动”的论点提供第二项证据。
本段作为一节的引言,起到了路线图的作用。它告诉读者,我们将从 5.1.1 节对“交易量构成”的分析,转向对“不同股票/交易日之间差异”的分析(即横截面和时间序列分析),这是论证的递进。第一项证据关注“是什么”,第二项证据关注“在哪里更强”。
假设你认为城市里的涂鸦都是一个叫“Zorro”的神秘艺术家画的。
- 5.1.1的论证: 你发现所有涂鸦都有一个共同的签名样式(周期性在成交笔数中最强)。
- 5.1.2的论证: 你的下一个逻辑步骤是去调查“Zorro”最喜欢在哪里活动。你猜测他喜欢在人流量大的街区作画。于是你去比较:
- 人流量大的街区 vs. 人迹罕至的小巷
- 周末 vs. 工作日
- 你发现,果然人流量越大的地方、在周末时间,“Zorro”的涂鸦就越多、越集中。
这个发现(涂鸦数量与人流量和时间正相关)就为“涂鸦是Zorro画的”提供了更有力的佐证。本节做的就是类似的事情:检验周期性的强度是否与算法交易的“人流量”(活跃度)正相关。
你怀疑某些湖里的鱼生病是因为一种特定的工业污染物。
- 5.1.1的证据: 你发现所有生病的鱼,血液里都含有一种特殊的化学物质(相当于周期性的“指纹”)。
- 5.1.2的证据: 你接着去采样不同湖泊的水。你将湖泊按“疑似污染程度”(算法交易代理指标)分为三类:重度污染、中度污染、清洁。你去这些湖里捕鱼,检查鱼的生病率(周期性强度)。
- 预期结果: 你会发现,重度污染湖里的鱼,生病率最高;清洁湖里的鱼,几乎不生病。
- 这个“污染越重、生病率越高”的规律,就是本节试图要证明的“算法交易越活跃、周期性越强”的逻辑。
📜 [原文10]
为了实现这一目标,我们需要一个统计量来总结每只股票在每个交易日的周期性强度。我们在第 4 节中记录了 fVRs 最高的频率在美国市场为 10 秒、15 秒、20 秒、30 秒、1 分钟和 5 分钟,在中国市场为 30 秒、1 分钟、2.5 分钟、5 分钟和 10 分钟(见图 3-4)。因此,对于每只股票 $s$ 在交易日 $d$,我们定义以下周期性强度代理指标:
- 定义核心变量的需求: 为了进行回归分析,需要一个因变量(Dependent Variable),也就是衡量“周期性强度”的指标。这个指标需要能够量化到“每只股票 $s$ 在每个交易日 $d$”这个精细的层面。
- 回顾关键频率: 作者回顾了第 4 节的发现(图3-4)。研究已经表明,周期性并非在所有频率上都存在,而是主要集中在几个特定的“热门”频率上。
- 美国市场: 10秒, 15秒, 20秒, 30秒, 1分钟, 5分钟。
- 中国市场: 30秒, 1分钟, 2.5分钟, 5分钟, 10分钟。
- 构建综合指标 (peri): 作者没有选择只用某一个频率(比如1分钟)的 fVR 作为代理指标,因为那样会丢失其他频率的信息。一个更稳健的做法是,将这些“热门”频率的 fVR 加总起来,形成一个综合性的强度指标。这个指标被命名为 $\text{peri}_{s,d}$。
- 解读公式 (9):
- $\text{peri}_{s,d}$ 是一个为股票 $s$ 在交易日 $d$ 计算的数值。
- 它的计算方式是“分情况讨论”:
- 如果股票 $s$ 是美国股票,就把该股票在该交易日的 10秒、15秒、20秒、30秒、1分钟、5分钟这六个频率的 fVR 值全部加起来。
- 如果股票 $s$ 是中国股票,就把该股票在该交易日的 30秒、1分钟、2.5分钟、5分钟、10分钟这五个频率的 fVR 值全部加起来。
- 指标的意义: $\text{peri}_{s,d}$ 这个值越高,说明在股票 $s$ 的交易日 $d$ 这一天,其交易量(成交笔数)在那些已知的关键周期性频率上的总能量占比越高,即整体的周期性现象越强。这个综合指标比单一频率的 fVR 更能全面地反映周期性的总体强度。
- 公式 (9):
- $\text{peri}_{s,d}$: 本文定义的核心因变量。代表股票 $s$ 在交易日 $d$ 的周期性总强度 (periodicity strength)。它是一个无单位的纯数值(百分比之和)。
- $s$: 股票的标识 (stock ticker)。
- $d$: 交易日的标识 (date)。
- $\mathrm{fVR}_{j, s, d}$: 代表股票 $s$ 在交易日 $d$ 这一天,其交易量时间序列在频率 $j$ 上的频率方差比 (Frequency Variance Ratio)。例如,$\mathrm{fVR}_{10\mathrm{s}, s, d}$ 就是10秒频率上的fVR。
- $:=$: 定义符号,表示左边由右边定义。
- {...: 分段函数的表示法,根据股票所属市场(美国或中国)选择不同的计算公式。
- 示例1: 一只活跃的美国股票 (AAPL)
- 日期:2021年10月5日
- 假设当天计算出AAPL在这6个频率上的fVR分别为:
- $\mathrm{fVR}_{10s} = 3.5\%$
- $\mathrm{fVR}_{15s} = 2.0\%$
- $\mathrm{fVR}_{20s} = 1.5\%$
- $\mathrm{fVR}_{30s} = 4.0\%$
- $\mathrm{fVR}_{1min} = 6.0\%$
- $\mathrm{fVR}_{5min} = 2.5\%$
- 则该股票当日的周期性强度指标为:
$\text{peri}_{\text{AAPL, 211005}} = 3.5\% + 2.0\% + 1.5\% + 4.0\% + 6.0\% + 2.5\% = 19.5\%$ (或写作 0.195)。
- 示例2: 一只不活跃的中国股票
- 日期:2021年10月5日
- 假设当天计算出该股票在这5个频率上的fVR分别为:
- $\mathrm{fVR}_{30s} = 0.3\%$
- $\mathrm{fVR}_{1min} = 0.5\%$
- $\mathrm{fVR}_{2.5min} = 0.4\%$
- $\mathrm{fVR}_{5min} = 0.6\%$
- $\mathrm{fVR}_{10min} = 0.8\%$
- (注意这些值都非常接近0.2%的基准)
- 则该股票当日的周期性强度指标为:
$\text{peri}_{\text{Stock, 211005}} = 0.3\% + 0.5\% + 0.4\% + 0.6\% + 0.8\% = 2.6\%$ (或写作 0.026)。
- 对比两个例子,19.5% >> 2.6%,清晰地表明AAPL当天的周期性远强于这只不活跃的中国股票。
- fVR的计算尺度: 这里需要注意一个计算细节。在第4节,fVR是基于多年平均的日内交易量序列计算的。但在这里,为了得到每个交易日的周期性强度,fVR必须在“日度”层面重新计算,即对每一天的日内交易量时间序列单独进行谱分解。这是一个计算量非常大的步骤。
- 选择频率的合理性: 这种方法的前提是,周期性主要就集中在这几个选定的频率上。如果某支股票的周期性主要体现在一个未被选中的频率(比如45秒),那么它的周期性强度就会被这个 $\text{peri}$ 指标低估。但由于这几个频率已经是全市场范围内最显著的,这种遗漏的风险相对较小。
本段定义了用于后续回归分析的关键因变量——周期性强度综合指标 $\text{peri}_{s,d}$。该指标通过加总各市场最主要的几个周期性频率上的频率方差比(fVR),为“每只股票在每个交易日”的周期性强度提供了一个量化、全面且合理的度量。
本段的目的是构建一个可操作、可量化的因变量,为后续的回归分析铺平道路。没有一个好的因变量,就无法进行严格的统计检验。定义 $\text{peri}_{s,d}$ 是从定性描述转向定量分析的关键一步,体现了实证研究的严谨性。
你是一名医生,想量化一位病人每天的“咳嗽严重程度”。
- fVR: 你发现病人的咳嗽声在某些特定音高(频率)上特别响。
- 关键频率: 你通过大量病例分析,知道这种病的咳嗽声主要集中在 100Hz, 150Hz, 200Hz 这三个音高上。
- 定义 peri 指标: 你决定将病人每天咳嗽声在这三个音高上的能量占比加起来,定义为当天的“咳嗽指数”。
- 咳嗽指数_d = 能量占比_100Hz,d + 能量占比_150Hz,d + 能量占比_200Hz,d
- 这个“咳嗽指数”就相当于 $\text{peri}_{s,d}$,它综合了最重要的几个方面,来给一个复杂的现象(咳嗽/ 周期性)打分。
你是一位音乐评论家,想给一首摇滚乐的“节奏感强度”打分。
- fVR: 你用频谱仪分析音乐,发现能量在鼓、贝斯、吉他的某些特定节奏点上很集中。
- 关键频率: 你知道摇滚乐的核心节奏通常是4/4拍里的小鼓(30秒)、底鼓(1分钟)和贝斯的固定音型(10秒)。
- 定义 peri 指标: 你把这首歌在“小鼓节奏”、“底鼓节奏”和“贝斯节奏”上的能量总和,作为这首歌的“节奏感分数”。
- 这个分数就是 $\text{peri}_{s,d}$。分数越高的歌,听起来“带劲”,节奏感越强。
📜 [原文11]
与第 4 节的方法(基于 2019-2021 年所有交易日平均的日内交易量时间序列的谱分解来估计 fVR)不同,这里我们需要每个交易日的 fVR,因为某些股票特征每天都在变化。结果,对于股票 $s$ 和交易日 $d$,我们基于该日日内交易量时间序列的谱分解来估计 $\mathrm{VR}_{j, s, d}$,其中这些 fVR 的第一个下标代表相应的频率。因此,对于每只股票 $s$,等式 (9) 定义了一个新的时间序列 $\left\{\text { peri }_{s, d}\right\}$,对于 $d=1,2, \ldots, D$。
- 点明计算方法的差异: 这段话的核心是强调本节计算 fVR 的方法与第 4 节的不同。
- 第 4 节的方法: 为了识别市场普遍的周期性模式,第4节采用了一种“求平均”的策略。它首先将一只股票在三年(2019-2021)内每一天的同一个时间点(比如所有天的上午9:30:01)的交易量求平均,得到一条“平均日”的日内交易量时间序列。然后对这条平滑过的“平均日”序列进行谱分解,估算 fVR。这样做的好处是滤除了每日的随机噪声,能更清晰地看到稳定存在的周期性模式。
- 本节的方法: 本节的目标是检验周期性强度与“每日变化的股票特征”之间的关系。因此,必须得到“每日”的周期性强度。所以,这里的计算方式是:对于每一只股票的每一个交易日,都单独拿出这一天的日内交易量时间序列(例如,从上午9:30到下午4:00的秒级成交笔数数据),然后对这条“单日”序列进行谱分解,估算出当天的 $\mathrm{fVR}_{j, s, d}$。
- 解释原因: “因为某些股票特征每天都在变化”。这是方法改变的根本原因。后面要用到的解释变量,比如每日的波动率、碎股成交量占比等,都是每天都不一样的。如果因变量(周期性强度)只有一个基于三年平均的值,而解释变量是每天都在变的日度数据,这两者就无法匹配,回归分析也无从谈起。为了让因变量和解释变量在时间维度上对齐(都是“股票-日度”层面),必须计算每日的 fVR。
- 重申变量定义:
- $\mathrm{fVR}_{j, s, d}$ 是基于股票 $s$ 在交易日 $d$ 单日的交易量数据计算出来的。
- 通过公式(9)的加总,对于每一只股票 $s$,我们都得到了一个新的时间序列:$\{\text{peri}_{s,1}, \text{peri}_{s,2}, \text{peri}_{s,3}, \ldots, \text{peri}_{s,D}\}$。这个序列记录了股票 $s$ 在样本期内每一天的周期性强度变化。
- 第4节的方法:
- 拿苹果公司(AAPL) 2019-2021年所有交易日的数据。
- 计算所有交易日上午9:30:01的平均成交笔数,得到一个值。
- 计算所有交易日上午9:30:02的平均成交笔数,得到另一个值。
- ... 以此类推,得到一条代表“平均交易日”的时间序列。
- 对这条序列做谱分析,得到一个单一的、代表AAPL这三年平均状况的 $\mathrm{fVR}_{1min}$ 值。
- 本节的方法:
- 拿AAPL在2021年10月5日这一天的成交笔数时间序列。
- 对这条序列做谱分析,得到一个 $\mathrm{fVR}_{1min, \text{AAPL}, 211005}$ 值。
- 拿AAPL在2021年10月6日这一天的成交笔数时间序列。
- 对这条序列做谱分析,得到一个 $\mathrm{fVR}_{1min, \text{AAPL}, 211006}$ 值。
- ... 以此类推,为每一天都计算一个fVR值,从而构成一个fVR的时间序列。
- 信噪比问题: 对单日数据进行谱分析,会受到当天特有事件(如重大新闻、市场情绪波动)产生的噪声影响,其结果不如对多年平均数据进行分析那么“干净”。估算出的 $\mathrm{fVR}_{j, s, d}$ 会有更大的波动性。然而,这种波动性正是研究想要捕捉和解释的,所以在这里是必要的。
- 计算成本: 这个方法需要对样本中的“股票数量 × 交易日数”条时间序列进行谱分解,计算量是巨大的。例如,3000支股票 × 3年 × 约250个交易日/年 = 2,250,000次谱分解运算。
本段详细阐述了为了匹配每日变化的解释变量,本节所采用的fVR计算方法与第4节的根本不同:即从对“多年平均日”序列的分析,转变为对“每个单日”序列的独立分析。这使得我们能够构建一个“股票-日度”的周期性强度时间序列 $\{\text{peri}_{s,d}\}$,作为后续回归分析的因变量。
本段的存在是为了澄清一个关键的方法论细节,避免读者产生混淆。通过明确对比两种fVR的计算方式及其各自的适用场景,作者展示了其研究设计的严谨性和逻辑性。向审稿人和读者表明,他们已经仔细考虑过数据处理的细节,并为后续的分析选择了最恰当的方法。
你想研究一个人的“每日学习效率”与“每日睡眠时间”的关系。
- 第4节的方法(不可行): 你把这个人三年来每天早上8:00的清醒度求了个平均值,8:01的清醒度也求平均... 得到一个“平均日”的清醒度曲线。你发现平均来看,他在上午10点效率最高。但这只有一个“平均效率最高点”,无法和“每日”的睡眠时间建立关系。
- 本节的方法(可行): 你记录下他第一天的学习效率曲线,并计算出当天的“峰值效率”。再记录第二天的曲线,计算第二天的“峰值效率”... 这样你就得到了一个每日的“峰值效率”序列。然后你就可以用这个序列去和“每日睡眠时间”序列做回归分析了。
本段解释的就是为什么要从“平均日分析”切换到“每日分析”。
你想知道每天的“交通拥堵程度”是否与当天的“天气”(晴天/雨天)有关。
- 第4节的方法: 你把一年中所有晴天的交通流量数据拿来,按时间点求平均,得到一条“平均晴天”的拥堵曲线。又得到一条“平均雨天”的拥堵曲线。你可以比较这两条曲线,得出“雨天比晴天更堵”的结论。但这是一种宏观比较。
- 本节的方法: 你需要更精细的数据。你计算出1月1日(雨天)的“拥堵指数”,1月2日(晴天)的“拥堵指数”,1月3日(晴天)的“拥堵指数”... 这样你有了一个每日的拥堵指数时间序列。然后你就可以进行回归分析,例如 拥堵指数 ~ 是否下雨 + 气温 + ...。
本段解释的就是为何要采用第二种方法,来构建每日的“拥堵指数”($\text{peri}_{s,d}$)。
📜 [原文12]
另一方面,我们遵循文献中广泛使用的代理指标,计算了衡量股票-日度水平的活动水平、交易效率和算法交易比例的几个特征。例如,Hendershott, Jones, and Menkveld (2011) 首先提出,每日消息数量的增加以及负的成交金额除以消息数量可以作为更高比例算法交易的代理指标。这一观点由 Boehmer, Fong, and Wu (2021) 和 Hatch et al. (2021) 进一步发展。O'Hara, Yao, and Ye (2014) 提出,相当一部分碎股是由算法交易员投放的。基于他们的观点,Weller (2018) 和 Erhard and Sloan (2020) 使用碎股成交量占比作为算法交易的代理指标。除了这些指标外,我们还在解释变量列表中增加了几个与波动率相关的指标,总结如下:
- 每日消息数量 (mess),
- 负的成交金额除以消息数量 (nvdmess),
- 碎股成交量占比 (oddrat),
- 1 分钟日内收益率的波动率 (vol),
- 2 与 2 分钟收益率方差与 1 分钟收益率方差之比之间的距离 (varrat)。
本段的目的是介绍即将用于回归分析的解释变量(Explanatory Variables),即用来解释周期性强度($\text{peri}_{s,d}$)变化的因素。作者明确指出,这些变量的选择不是凭空想象的,而是“遵循文献中广泛使用的代理指标”,这大大增强了研究的科学性和可信度。
- 介绍变量的三个维度: 这些解释变量主要从三个方面来刻画股票在日度水平的特征:
- 活动水平 (Activity Level): 股票交易的活跃程度。
- 交易效率 (Trading Efficiency): 价格反映信息的速度和准确性。
- 算法交易比例 (Proportion of Algorithmic Trading): 算法交易在这只股票/这一天的交易中占多大比重。这三者紧密相关,很多指标可以同时反映多个维度。
- 详细介绍每个代理指标及其文献来源:
- 每日消息数量 (mess - messages):
- 定义: “消息”在这里通常指提交到交易所的订单(包括限价单、市价单)和订单的修改、取消等行为的总和。它反映了市场的整体信息流和交易意愿的活跃度。
- 与算法交易的关系: 算法交易,特别是高频交易,其特点就是通过程序高速、大量地提交、修改和取消订单来捕捉微小的交易机会。因此,一只股票的“消息数量”越多,通常意味着算法交易越活跃。
- 文献来源: Hendershott, Jones, and Menkveld (2011) 是这个领域的开创性论文,他们首次使用这个指标作为算法交易的代理。
- 负的成交金额除以消息数量 (nvdmess - negative volume per message):
- 定义: 这个指标有点复杂。首先计算成交金额 / 消息数量,得到每条消息平均对应的成交额。因为算法交易倾向于下小订单,所以这个比值越小,算法交易比例被认为越高。取负号 - 是一个技术处理,使得这个指标与算法交易比例正相关(因为原始比值越小,负值就越大)。
- 与算法交易的关系: 算法交易消息多但单笔成交小,所以 成交金额/消息数量 很小。非算法交易消息少但单笔成交大,所以 成交金额/消息数量 很大。因此,nvdmess 越大,代表算法交易比例越高。
- 文献来源: 同样源于 Hendershott, Jones, and Menkveld (2011),并被后续研究者如 Boehmer, Fong, and Wu (2021) 等发展。
- 碎股成交量占比 (oddrat - odd-lot ratio):
- 定义: “碎股”(Odd Lot)通常指交易量不是整百股(如100, 200...)的交易,比如交易25股。oddrat 就是碎股交易的成交量占总成交量的比例。
- 与算法交易的关系: 算法交易在拆分订单时,会产生大量非整百股的小额订单,即碎股。此外,一些高频交易策略也通过碎股交易来探测市场流动性。因此,oddrat 越高,通常意味着算法交易越活跃。
- 文献来源: O'Hara, Yao, and Ye (2014) 首先系统研究了碎股与算法交易的关系,后续的 Weller (2018) 等人将其用作代理指标。
- 1分钟日内收益率的波动率 (vol - volatility):
- 定义: 计算当天所有1分钟收益率的标准差,用来衡量股价的日内波动率。
- 与算法交易的关系: 关系比较复杂。一方面,高波动率可能吸引算法交易(因为有套利机会);另一方面,算法交易的活动本身也可能引发波动率。通常预期,算法交易活跃的环境下,波动率也较高。
- 2与2分钟收益率方差与1分钟收益率方差之比之间的距离 (varrat - variance ratio distance):
- 定义: 这个指标基于 Lo and MacKinlay (1988) 的方差比检验。理论上,如果股价服从随机游走(即市场是完全有效的),那么2分钟收益率的方差应该是1分钟收益率方差的2倍,即 Var(r_2min) / Var(r_1min) = 2。varrat 衡量的是 | Var(r_2min) / Var(r_1min) - 2 |,即实际的方差比与理论值2的偏离程度。
- 与交易效率和算法交易的关系: 大量的研究表明,算法交易可以通过快速套利来消除价格的短期可预测性,从而提高市场的价格效率,使股价行为更接近随机游走。因此,算法交易越活跃,方差比就越接近2,varrat 这个偏离值就越小。所以,varrat 与算法交易比例预期是负相关的。
- 指标的多重解释性: vol(波动率)的解释不是单向的。它既是算法交易的原因,也可能是其结果,存在内生性问题。作者在后面也提到了这一点。
- 不同市场的适用性: 碎股的定义在美国市场(小于100股)和中国市场(A股交易单位为“手”,1手=100股)有所不同,在应用时需要根据市场规则进行调整。
- 数据的可得性: 计算 mess 和 nvdmess 需要高频的订单簿数据(Quote and Trade data),这种数据的获取和处理成本非常高。
本段系统地介绍了用于解释周期性强度的五个关键解释变量(mess, nvdmess, oddrat, vol, varrat)。作者详细说明了每个变量的定义、其与算法交易或市场效率的理论联系,并列举了支持其作为代理指标的权威学术文献,为后续的回归分析提供了坚实的理论基础和变量选择依据。
本段的目的是构建回归模型中的自变量集合。通过详细阐述这些变量的选择依据和理论背景,作者向读者证明了其模型设定的合理性。这是实证研究中非常重要的一步,一个好的模型不仅需要有可靠的因变量,更需要有理论支撑的、被广泛接受的自变量。
你是一名侦探,想要通过一个人的日常行为来推断他是不是一个“电脑高手”(算法交易员)。你选择了以下几个“代理指标”:
- mess: 他每天敲击键盘的次数。电脑高手通常敲键盘更多。
- nvdmess: 他每天“打开的软件数量”和“实际完成的工作量”的比值。电脑高手可能打开很多窗口和工具,但每个都是为了完成一个大任务中的一小步,所以这个比值可能和普通人不一样。
- oddrat: 他使用快捷键的频率。电脑高手更倾向于用快捷键而不是鼠标。
- vol: 他一天中情绪的波动程度。可能因为调试代码而大起大落。
- varrat: 他完成任务的效率。电脑高手完成一系列小任务的总时间,与他完成一个大任务的时间,其比例可能更符合最优规划。
通过观察这些指标,你可以间接地对“他是否是电脑高手”做出一个概率判断。
你想判断一个池塘的“生态健康程度”(周期性强度),但你不能直接测量。你选择观察以下几个代理指标(解释变量):
- mess: 池塘里水生昆虫的总数量。
- nvdmess: 池塘里鱼的平均大小。
- oddrat: 池塘里稀有水生植物的比例。
- vol: 一天内水温的变化范围。
- varrat: 池塘水体的清澈度。
通过综合分析这些指标,你可以推断出池塘的生态健康状况。本段就是在定义这些用于推断“算法交易活跃度”的“生态指标”。
📜 [原文13]
我们对所选的解释变量列表提供几点说明。mess 描述了股票在市场中的交易活动水平。它也是算法交易的一个代理指标,因为算法交易员往往比其他投资者发送更多数量的订单。nvdmess 是每条消息的负平均交易量,它与算法交易的比例正相关,因为算法交易员倾向于下小额订单。类似地,oddrat 与算法交易的比例正相关,因为它衡量了来自碎股的交易量比例,而碎股通常被认为最常由高频/算法交易员投放以减少订单影响。变量 vol 表征了波动率。最后,varrat 基于 Lo and MacKinlay (1988) 的方差比检验。2 分钟收益率和 1 分钟收益率的方差比表征了价格对随机游走的偏离 [^16],该比率对 2 的偏离衡量了标的股票的价格效率。因为算法交易倾向于提高价格效率 (Hendershott, Jones, and Menkveld, 2011, Conrad, Wahal, and Xiang, 2015; Clark-Joseph, Ye, and Zi, 2017, Boehmer, Fong, and Wu, 2021),varrat 往往与算法交易的比例负相关。
这一段是对上一段列出的五个解释变量进行更详细的解释和总结,特别是阐明它们与算法交易之间的预期关系(正相关或负相关),为读者理解接下来的回归结果表格做铺垫。
- mess (每日消息数量):
- 双重角色: 它既是“交易活动水平”的直接度量,也是“算法交易”的代理指标。
- 核心逻辑: 算法交易员是“消息”的主要产生者,因为他们的策略依赖于高速、大量的订单操作。因此,mess 越高,算法交易比例预期越高。预期关系:正相关 (+)。
- nvdmess (每条消息的负平均交易量):
- 核心逻辑: 算法交易员的特点是“订单拆分”,即用大量的小额订单来执行一个大意图。这导致他们的“消息数量”很多,但分摊到每条消息上的“平均交易量”很小。回顾其定义:nvdmess = - (成交金额 / 消息数量)。
- 算法交易员: 消息数量大,成交金额/消息数量小。
- 非算法交易员: 消息数量小,成交金额/消息数量大。
- 因此,成交金额/消息数量越小,算法交易比例越高。
- 取负号后,nvdmess 越大,算法交易比例越高。
- 预期关系:正相关 (+)。
- oddrat (碎股成交量占比):
- 核心逻辑: 碎股(非100股整数倍的交易)是算法交易执行订单拆分和探测流动性时的常见产物。散户也可能产生碎股,但高频/算法交易员是系统性、大规模产生碎股的主力军。因此,oddrat 越高,算法交易比例预期越高。
- 预期关系:正相关 (+)。
- vol (波动率):
- 核心逻辑: vol 只是一个衡量价格波动剧烈程度的控制变量,它与算法交易的关系是双向的,不明确。但通常算法交易在波动率高的环境中更活跃。因此,也预期一个正向关系。
- 预期关系:正相关 (+) (尽管可能存在内生性)。
- varrat (方差比偏离度):
- 核心逻辑: varrat 衡量的是股价偏离随机游走的程度,是价格效率的反向指标(varrat 越小,价格效率越高)。
- 文献共识: 大量文献(如HJM(2011), BFW(2021)等)表明,算法交易通过其快速的信息处理和套利能力,能有效消除市场中的微小定价偏差,从而“提高价格效率”。
- 推论: 算法交易比例越高 -> 价格效率越高 -> varrat 越小。
- 预期关系:负相关 (-)。
- 符号的理解: 理解 nvdmess 和 varrat 与算法交易比例的关系是关键。nvdmess 是正相关,而 varrat 是负相关。如果在回归中看到 varrat 的系数是负的,这恰恰支持了算法交易驱动周期性的假设。
- 控制变量的角色: vol 和 varrat 不仅是算法交易的代理,它们本身也代表了重要的市场状态(波动率和效率),将它们放入回归模型中,可以帮助分离出其他代理指标(如mess, oddrat)的纯粹影响,起到了控制变量的作用。
- [^16]: 注脚16可能指向对随机游走模型的更详细解释或参考文献,对于深入理解varrat指标很重要。
本段对五个解释变量逐一进行了详细的功能说明和逻辑梳理,明确了每个变量与算法交易比例之间的预期关系(mess+, nvdmess+, oddrat+, vol+, varrat-)。这为后续解读回归结果中的系数符号(正或负)提供了理论依据和判断标准。
本段的目的是为非专业的读者提供一个清晰的“变量说明书”。在展示充满数字和星号的回归表格之前,必须先让读者明白每个变量是什么意思,以及为什么预期它的系数是正的还是负的。这极大地降低了后续内容的理解门槛,是良好学术写作的体现。
你是一名篮球教练,想通过数据分析来识别哪个球员是“神射手”(算法交易员)。你建立了回归模型 比赛得分 ~ X1 + X2 + X3 + ...,其中 X 是球员的技术统计。本段就在解释这些 X:
- mess (出手次数): 神射手通常被赋予更多出手权。预期正相关。
- nvdmess (每次出手前的平均运球次数的负数): 神射手倾向于“接球就投”,运球少。所以“平均运球次数”和“神射手”属性负相关,其负数就正相关。
- oddrat (三分球出手占比): 神射手的主要武器是三分。预期正相关。
- vol (得分的稳定性): 控制变量。
- varrat (罚球命中率与80%的差距): 神射手基本功扎实,罚球命中率非常接近理论最优值(比如80%),所以差距小。预期负相关。
- 通过这段解释,当球探(读者)看到回归结果中“三分球出手占比”的系数是正的,“罚球命中率差距”的系数是负的,他们就能理解“哦,这确实符合我们对神射手的认知”。
你在做一个“猜职业”的游戏。屏幕上有一个人的信息(解释变量),你要猜他是不是“程序员”(算法交易员)。本段就是告诉你每个信息的解读方法:
- mess (每日使用电脑时长): 越长,是程序员的可能性越大 (+)。
- nvdmess (每日喝咖啡的杯数): 越多,是程序员的可能性越大 (+)。(这里假设程序员喝咖啡多)
- oddrat (格子衬衫占衣柜的比例): 越高,是程序员的可能性越大 (+)。(刻板印象)
- vol (每天工作开始和结束时间): 控制变量。
- varrat (发际线高度与平均值的差): 差值越大(越高),是程序员的可能性越大 (+)。(另一个刻板印象)
- 这段解释让你在看到具体数据时,能够正确地解读信息并做出判断。
📜 [原文14]
利用这些解释变量和响应变量 $peri_{s, d}$,我们运行以下具有不同固定效应的回归:
- 构建回归模型: 本段正式提出了用于检验假设的面板数据回归模型。
- 响应变量/因变量 (Response/Dependent Variable): $peri_{s,d}$,即我们之前定义的,代表股票 $s$ 在交易日 $d$ 的周期性总强度。
- 解释变量/自变量 (Explanatory/Independent Variables): $mess_{s,d}$, $nvdmess_{s,d}$, $oddrat_{s,d}$, $vol_{s,d}$, $varrat_{s,d}$,即上一段介绍的五个衡量算法交易活跃度和市场状态的代理指标。
- 模型形式: 是一个线性回归模型。它假设周期性强度 $peri_{s,d}$ 可以由这五个解释变量的线性组合来解释。
- 解读公式 (10):
- $\text{peri}_{s,d} \sim ...$: “$\sim$”符号在这里表示“由...进行回归”或“被...建模”。它表示左边的因变量与右边的自变量们之间的关系。
- $\beta_1, \beta_2, \beta_3, \beta_4, \beta_5$: 这些是回归系数。它们是模型要估计的核心参数。每个系数 $\beta_i$ 代表在控制其他所有变量不变的情况下,对应的自变量 $X_i$ 每增加一个单位,因变量 $peri_{s,d}$ 平均会变化多少。
- 我们的目标: 就是要看这些 $\beta$ 系数的符号、大小和统计显著性。根据上一段的分析,我们预期 $\beta_1, \beta_2, \beta_3, \beta_4$ 是正的,而 $\beta_5$ 是负的。如果回归结果真的如此,就强有力地支持了我们的假设。
- 引入“固定效应” (Fixed Effects):
- 什么是固定效应: 这是一个处理面板数据(同时有横截面维度-股票,和时间序列维度-日期)时至关重要的技术。在我们的数据中,可能存在一些难以观测或量化,但又会影响周期性强度的因素。
- 股票固定效应 (Stock Fixed Effects): 控制那些不随时间变化,但因股票而异的特征。例如,某些行业(如科技股)的股票本身就比其他行业(如公共事业股)更受算法交易青睐。加入股票固定效应,就相当于为每只股票设置一个单独的截距项,从而剔除了这些股票固有属性的影响,使得我们能更纯粹地看到变量在时间上的变化如何影响周期性。
- 日期固定效应 (Date Fixed Effects): 控制那些不因股票而异,但随时间变化的共同冲击。例如,某一天美联储宣布加息,这个事件会影响市场上所有的股票。加入日期固定效应,就相当于为每个交易日设置一个单独的截距项,从而剔除了这些宏观事件的影响,使得我们能更纯粹地看到变量在股票之间的差异如何影响周期性。
- 为什么使用不同固定效应: 作者运行了多个版本的回归:无固定效应、只有股票固定效应、只有日期固定效应、以及同时有股票和日期固定效应。这是一种稳健性检验。如果结论在所有这些不同的模型设定下都成立,那么这个结论就非常可信,不容易被“遗漏变量偏误”所攻击。最严格、最可信的结果通常来自同时包含股票和日期固定效应的模型。
- 公式 (10):
- $\text{peri}_{s,d}$: 因变量,股票s在日期d的周期性强度。
- $\text{mess}_{s,d}, \text{nvdmess}_{s,d}, \dots$: 自变量,股票s在日期d的各项特征值。
- $\beta_1, \dots, \beta_5$: 待估计的回归系数。
- 完整的模型表达式 (以包含双重固定效应为例) 应该是:
其中:
- $\alpha_s$: 股票固定效应,代表股票 $s$ 的固有平均周期性水平。
- $\gamma_d$: 日期固定效应,代表日期 $d$ 这一天的市场平均周期性水平。
- $\epsilon_{s,d}$: 随机误差项。
公式 (10) 是一个简化写法,省略了截距项、固定效应项和误差项。
假设回归分析后,得到 $\beta_1$ (对应 mess) 的估计值为 0.0008,并且是统计显著的。
- 解释: 在控制了其他四个变量以及任何固定效应后,一只股票在一天的mess(每日消息数量,假设已经标准化)每增加1个单位(例如,1个标准差),其周期性强度指标 peri 平均会增加 0.0008。
- 结论: mess与peri之间存在显著的正相关关系。这与我们的预期相符,即消息数量越多的股票,周期性越强。
- 变量标准化: 在进行回归之前,通常会对所有变量(因变量和自变量)进行标准化处理(减去均值,除以标准差)。这样做的好处是使得回归系数的大小可以直接比较,表示自变量变化一个标准差,因变量变化多少个标准差。表格的注释中也提到了这一点。
- 标准误的聚类 (Clustering): 面板数据中,同一只股票在不同日期的误差项可能相关,同一天不同股票的误差项也可能相关。为了得到更准确的系数显著性检验结果,需要在股票层面和/或日期层面进行聚类标准误调整。表格的注释中也提到了这一点。
本段正式给出了用于检验核心假设的面板数据回归模型(公式 10)。该模型旨在量化五种算法交易代理指标及控制变量与周期性强度指标 $peri_{s,d}$ 之间的关系。作者还强调将使用不同的固定效应设定来确保结果的稳健性,这体现了现代计量经济学研究的严谨标准。
本段的目的是将前面所有的准备工作(定义因变量、选择自变量)最终汇总成一个具体的、可执行的计量模型。它是连接理论假设和实证结果的桥梁。没有这个明确的模型设定,后面的回归表格就无从谈起。
你想建立一个模型来预测一个学生的“期末考试成绩”($peri$)。你选择了几个预测指标(解释变量):
- mess: “每天的学习时长”
- nvdmess: “每天做的练习题数量”
- oddrat: “上课的听讲专注度”
- vol: “每天情绪的波动”
- varrat: “作业的完成质量”
公式(10)就是 考试成绩 ~ β1学习时长 + β2练习题数 + ...。
固定效应就是:
- 学生固定效应: 控制学生本身智商、基础等不随时间变化的因素。
- 日期固定效应: 控制考试前一天学校是否停电、食堂饭菜是否可口等对所有学生都有影响的共同因素。
通过这个带有固定效应的模型,你可以更准确地知道“学习时长”到底对“成绩”有多大的净影响。
你正在用一个复杂的均衡器(回归模型)来调试音响系统,目标是让“音乐的清晰度”($peri$)达到最佳。
- 解释变量: 均衡器上有很多推子,比如“低音”(mess),“中音”(nvdmess),“高音”(oddrat)等。
- 回归系数β: 每个推子向上或向下推会对“清晰度”产生多大的影响。
- 固定效应:
- 歌曲固定效应 (股票F.E.): 不同的歌曲(古典、摇滚、流行)本身录音质量就不同。控制这个效应,你才能知道均衡器的调整对任何歌曲的普适效果。
- 环境固定效应 (日期F.E.): 在不同的房间(客厅、卧室)或不同的时间(白天、晚上)听,背景噪音不同。控制这个效应,你才能知道均衡器本身的性能。
本段就是告诉你,他们设计了一个非常精密的均衡器,并且考虑了歌曲和环境的影响,来精确测量每个推子的作用。
📜 [原文15]
表 2 总结了美国市场(面板 A)和中国市场(面板 B)股票的回归 (10) 的结果。
[^9]表 2:周期性强度 $peri_{s, d}$ 对股票层面特征的回归结果,具有不同的固定效应 (F.E.)。所有变量都通过其均值和标准差进行了标准化。估计系数在 1% ()、5% () 或 10% () 水平上显著。标准误是基于股票层面的股票 F.E.、日度层面的日度 F.E. 以及股票和日度层面的股票和日度 F.E. 聚类计算的。这里我们报告了“组内 $R^{2}$”,它衡量了每个固定效应面板内解释的方差。最后一列显示了从“算法交易员”解释中推断出的系数符号。
| 无 F.E. | 股票 F.E. | 日度 F.E. | 股票 & 日度 F.E. | 从“算法交易员”解释中推断出的符号 | |
|---|---|---|---|---|---|
| 面板 A: 美国市场 | |||||
| mess | $-9.51 \times 10^{-4}$ | $5.93 \times 10^{-4 * * *}$ | $9.42 \times 10^{-4 * * *}$ | $8.74 \times 10^{-4 * * *}$ | + |
| nvdmess | $1.14 \times 10^{-3 * *}$ | $-2.59 \times 10^{-5}$ | $2.10 \times 10^{-4 * * *}$ | $5.67 \times 10^{-5 *}$ | + |
| oddrat | $1.67 \times 10^{-3 * *}$ | $2.67 \times 10^{-4 * * *}$ | $4.66 \times 10^{-4 * * *}$ | $5.62 \times 10^{-4 * * *}$ | + |
| vol | $-2.22 \times 10^{-4}$ | $-2.33 \times 10^{-5}$ | $2.35 \times 10^{-5}$ | $3.45 \times 10^{-5}$ | + |
| varrat | $-2.92 \times 10^{-3 * * *}$ | $-7.03 \times 10^{-5 * * *}$ | $-5.95 \times 10^{-5 * * *}$ | $2.76 \times 10^{-5 * *}$ | - |
| $R^{2}$ | 3% | 1% | 2% | 1% | |
| 面板 B: 中国市场 | |||||
| mess | $3.01 \times 10^{-3 * * *}$ | $3.00 \times 10^{-3 * * *}$ | $2.88 \times 10^{-3 * * *}$ | $3.13 \times 10^{-3 * * *}$ | + |
| nvdmess | $1.19 \times 10^{-3 * * *}$ | $3.14 \times 10^{-4 * * *}$ | $4.88 \times 10^{-5 *}$ | $4.83 \times 10^{-4 * * *}$ | + |
| oddrat | $7.49 \times 10^{-4 * *}$ | $6.95 \times 10^{-4 * * *}$ | $1.24 \times 10^{-3 * * *}$ | $6.62 \times 10^{-4 * * *}$ | + |
| vol | $7.59 \times 10^{-4 * * *}$ | $1.94 \times 10^{-3 * * *}$ | $2.16 \times 10^{-3 * * *}$ | $2.17 \times 10^{-3 * * *}$ | + |
| varrat | $-6.80 \times 10^{-4 * * *}$ | $-5.67 \times 10^{-5 * * *}$ | $-1.60 \times 10^{-4 * * *}$ | $-1.38 \times 10^{-4 * * *}$ | - |
| $R^{2}$ | 13% | 16% | 15% | 16% |
这部分是对表2的详细解读,这是本节的核心证据。
- 表格结构:
- 两大面板 (Panel): 面板A是美国市场的结果,面板B是中国市场的结果。分开展示便于比较两国市场的异同。
- 行 (Rows): 每一行对应一个解释变量(mess, nvdmess, oddrat, vol, varrat)或模型的统计量($R^2$)。
- 列 (Columns):
- 第一列是变量名。
- 中间四列是四种不同的回归模型设定,从左到右控制越来越严格:
- 无 F.E.: 普通最小二乘回归(Pooled OLS),未控制任何固定效应。结果最不可靠。
- 股票 F.E.: 只控制了股票固定效应。
- 日度 F.E.: 只控制了日期固定效应。
- 股票 & 日度 F.E.: 同时控制两种固定效应。这是最严格、最可信的模型。
- 最后一列是理论上预期的系数符号,用于快速比对。
- 如何阅读表格内容:
- 数值: 每个单元格里的数值是估计出的回归系数 $\beta$。由于变量已标准化,它可以解释为自变量增加一个标准差,因变量peri变化的数量。
- 星号 *: 代表统计显著性水平。
- ***: 在1%的水平上显著。意味着我们有99%的把握认为这个系数不为零。这是非常强的显著性。
- **: 在5%的水平上显著。95%的把握。
- *: 在10%的水平上显著。90%的把握。
- 没有星号:不显著,我们不能拒绝“系数为零”的原假设,即该变量与peri没有稳定的线性关系。
- $R^2$ (R-squared): 衡量模型解释力的指标。这里的“组内 $R^2$” (Within $R^2$)是固定效应模型特有的,表示模型解释了在每个股票/日期组内部,因变量方差的百分之几。值比较低(1%-16%)是金融学研究中非常正常的,因为金融市场充满了噪音。
- 解读面板A:美国市场:
- 关注最严格模型 (股票 & 日度 F.E. 列):
- mess: 系数为正 ($+8.74 \times 10^{-4}$),且*极显著。符合预期(+)。消息越多,周期性**越强。
- nvdmess: 系数为正 ($+5.67 \times 10^{-5}$),但仅*10%显著。方向符合预期(+),但关系稍弱。
- oddrat: 系数为正 ($+5.62 \times 10^{-4}$),且*极显著。符合预期(+)。碎股占比越高,周期性**越强。
- vol: 系数为正 ($+3.45 \times 10^{-5}$),但不显著。说明在控制其他变量后,波动率本身与周期性没有清晰的线性关系。这可能源于其内生性。
- varrat: 系数为正 ($+2.76 \times 10^{-5}$),且5%显著。这与预期的负号(-)不符! 这是一个异常点,作者在下文会进行讨论。它可能意味着在美国市场,算法交易对价格效率**的影响机制更复杂,或者varrat这个代理指标在美国市场的有效性存疑。
- 解读面板B:中国市场:
- 关注最严格模型 (股票 & 日度 F.E. 列):
- mess: 系数为正 ($+3.13 \times 10^{-3}$),*极显著。符合预期(+)**。
- nvdmess: 系数为正 ($+4.83 \times 10^{-4}$),*极显著。符合预期(+)**。
- oddrat: 系数为正 ($+6.62 \times 10^{-4}$),*极显著。符合预期(+)**。
- vol: 系数为正 ($+2.17 \times 10^{-3}$),*极显著。符合预期(+)。波动率越高,周期性**越强。
- varrat: 系数为负 ($-1.38 \times 10^{-4}$),*极显著。完美符合预期(-)。价格效率越高(varrat越小),周期性**越强。
- 综合结论:
- 在中国市场,所有算法交易代理指标的系数符号都完美地符合理论预期,并且高度显著。
- 在美国市场,大多数代理指标(mess, nvdmess, oddrat)也基本符合预期,但varrat出现了意外的正号。
- 总体来看,结果在很大程度上支持了“算法交易活跃度越高的股票和交易日,周期性越强”的假说。
- 看中国市场最严格模型中 mess 的系数:$3.13 \times 10^{-3}$。
- 解释: 在中国市场,控制了其他四个变量以及股票和日期的固定效应后,如果一只股票某一天的mess(标准化消息数量)比它自己的平均水平高出一个标准差,那么它当天的peri(标准化周期性强度)预计会高出 $0.00313$ 个标准差。这是一个显著的正向影响。
- 忽略固定效应的重要性: 如果只看“无 F.E.”列,美国市场 mess 的系数甚至是负的,这很可能是由遗漏变量偏误导致的错误结论。固定效应模型的结果才是可靠的。
- 如何看待不一致的结果 (varrat in US): 科学研究并非总能得到完美一致的结果。这个异常的 varrat 系数本身就是一个有趣的发现,值得深入探讨。它并不推翻整体结论,因为其他主要代理指标都支持假设,但它揭示了问题的复杂性。
- 经济显著性 vs. 统计显著性: 系数很小(例如$10^{-4}$级别),但因为变量都标准化了,这个大小是有意义的。同时,即使系数小,只要统计上显著(有星号),就说明关系是稳定的。
表2通过面板数据回归分析,系统地检验了周期性强度与一系列算法交易代理指标之间的关系。结果在很大程度上证实了二者之间存在显著的正相关关系(mess, nvdmess, oddrat为正,中国市场的varrat为负),为“周期性由算法交易驱动”的假说提供了强有力的统计证据,尤其是在中国市场,证据链条非常完整。
表格是实证论文的核心。表2的存在,就是将之前所有的理论、假设和模型设定,最终落到可检验的数据结果上。它是本节(5.1.2)论点的直接证据,通过展示具体的回归系数和显著性水平,将论证从定性推测提升到了定量证实的高度。
这是“猜职业”游戏的结果报告。模型要猜一个人是不是“程序员”。
- 面板A(美国程序员) vs. 面板B(中国程序员)
- 回归结果:
- “每日喝咖啡杯数”(nvdmess)在中国程序员中和“程序员”属性显著正相关,但在美国程序员中关系不那么强。可能美国程序员也爱喝别的。
- “发际线高度”(varrat)在中国程序员中和“程序员”属性显著正相关(负的系数意味着发际线越低,程序员属性越弱),但在美国程序员中出现了意外的反向关系。可能美国程序员更注重保养。
- 但“每日使用电脑时长”(mess)和“格子衬衫比例”(oddrat)在两国程序员中都和“程序员”属性显著正相关。
- 结论: 尽管存在一些文化差异(市场差异),但核心指标都表明,我们的代理变量能很好地识别出“程序员”这个群体。
📜 [原文16]
美国市场中的大多数变量和中国市场中的所有变量都表明,算法交易与交易量中的周期性模式正相关。特别是,对于具有更高算法交易比例(由 mess、nvdmess 和 oddrat 衡量)以及更高价格效率水平(由负的 varrat 衡量)的股票和交易日,我们观察到更强的周期性 [^17]。具体而言,随着标准化的 mess、nvdmess、oddrat 或负的 varrat 增加一个单位,标准化的 peri 值平均增加约 $5 \times 10^{-5}-3 \times 10^{-3}$,其中 mess 的影响最大。
本段是对表2回归结果的文字总结和解读。
- 总体结论: “美国市场中的大多数变量和中国市场中的所有变量都表明,算法交易与交易量中的周期性模式正相关。” 这是对整个表2最核心的概括。
- 中国市场: 结论非常干净利落,所有变量都符合预期。
- 美国市场: “大多数变量”符合预期,承认了存在 varrat 这样的例外。这种表述是客观和严谨的。
- 详细阐述正相关关系: 作者进一步解释了“正相关”的具体含义。
- 更高算法交易比例: 这是由 mess (消息多)、nvdmess (每消息成交量小)、oddrat (碎股多) 这三个指标的正系数来体现的。这些指标值越高,意味着算法交易越活跃。
- 更高价格效率水平: 这是由 varrat 的负系数来体现的(主要在中国市场)。varrat 越小(即负的 varrat 越大),价格效率越高。
- 结论: 在算法交易更活跃、价格效率更高(这本身也是算法交易的结果)的股票和交易日,peri 值(周期性强度)也更高。
- 量化影响大小: “具体而言... peri 值平均增加约 $5 \times 10^{-5}-3 \times 10^{-3}$”。
- 这句话试图给出一个回归系数影响大小的直观范围。作者查看了表2中所有显著且符合预期的系数(例如,mess 的系数约为 $3 \times 10^{-3}$,oddrat 的系数约为 $6 \times 10^{-4}$,nvdmess 约为 $5 \times 10^{-5}$ 等),然后给出了一个大致的区间。
- 这个范围 $5 \times 10^{-5}$ 到 $3 \times 10^{-3}$ 表示,当一个标准化的算法交易代理指标增加一个标准差时,标准化的周期性强度 peri 大约会增加 0.00005 到 0.003 个标准差。
- “其中 mess 的影响最大”。通过比较系数的绝对值,可以看到 mess 的系数(在中国市场是 $3.13 \times 10^{-3}$)通常是最大的,这意味着在所有代理指标中,消息数量的增加对周期性强度的提升效果最显著。
- 脚注[^17]: 这个脚注可能包含对 varrat 在美国市场结果异常的进一步讨论,或者对价格效率与算法交易关系的更多参考文献。
让我们重新审视上一节的例子:
- 中国市场 mess 的系数是 $3.13 \times 10^{-3}$ (即 0.00313)。
- 美国市场 oddrat 的系数是 $5.62 \times 10^{-4}$ (即 0.000562)。
- 美国市场 nvdmess 的系数是 $5.67 \times 10^{-5}$ (即 0.0000567)。
这些数值都落在作者给出的 $5 \times 10^{-5}$ 到 $3 \times 10^{-3}$ 这个区间内。mess 的 $3.13 \times 10^{-3}$ 确实是其中影响较大的。
- 系数大小的比较: 只有当所有变量都经过标准化后,才能直接比较系数的大小来判断影响力的强弱。表格注释已经确认了这一点。
- 经济意义: 尽管数值看起来很小,但在金融市场这种高度随机的环境中,能够稳定地识别出这种幅度的影响已经非常不容易。一个变量变化1个标准差,能引起另一个变量稳定地变化0.003个标准差,在巨大的样本量下,这已经构成了显著的经济意义。
本段用通俗的语言总结了表2复杂的回归结果,强调了算法交易代理指标与周期性强度之间普遍存在的正相关关系。通过量化影响范围并指出mess是影响力最大的指标,使得回归结果的含义更加清晰和直观。
本段的目的是将表格化的数据结果“翻译”成流畅的文字叙述。不是所有读者都有耐心或能力去仔细解读回归表格,这段总结为他们提供了核心结论的“摘要版”。它在论证链条中承上启下,确认了第二项证据(相关性证据)的成立,并为下一小节的讨论做铺垫。
这是对“猜程序员”游戏结果的总结报告:
“我们的模型显示,在中国和美国,‘每日使用电脑时长’(mess) 和 ‘格子衬衫比例’(oddrat) 都是预测一个人是不是程序员的强有力指标。具体来说,当这些指标每增加一个标准差时,‘是程序员’的概率分数会增加0.05%到0.3%不等,其中‘每日使用电脑时长’的影响最大。”
这段话就是对一个复杂数据表格的简明解释。
你是一位农业科学家,研究不同因素对“水稻产量”(peri)的影响。在分析了大量数据后,你向农民们做报告:
“总的来说,我们的研究表明,‘施氮肥的量’(mess) 和 ‘灌溉水的纯净度’(oddrat) 都和水稻增产显著正相关。具体来说,每多施一单位标准化的氮肥,水稻产量大约能增加0.3%个标准差。在所有因素里,氮肥的影响是最大的。”
这段总结将复杂的农业实验数据,转化为了农民能听懂的、可操作的结论。
📜 [原文17]
[^10]总体而言,几乎所有变量的估计回归系数在统计上都是显著的,它们的符号表明周期性强度与股票的活动水平、交易效率以及算法交易比例正相关。我们强调,这项分析并没有提供关于解释变量是否引起周期性的因果陈述,因为例如,算法交易的水平也可能与市场中的流动性和价格冲击内生相关。尽管如此,这项分析与算法交易在两个市场中都与周期性交易行为正相关的解释是一致的。
- 再次总结结果: “总体而言,几乎所有变量的估计回归系数在统计上都是显著的,它们的符号表明...正相关。” 这句话是对结论的又一次强化和确认。作者强调了两点:
- 统计显著性: 大部分系数旁边都有星号,表明这些关系不是随机出现的,而是稳定的。
- 符号一致性: 系数的符号(正或负)与理论预期高度一致,共同指向一个结论:周期性强度与股票的活动水平、交易效率、算法交易比例正相关。
- 强调相关非因果: “我们强调,这项分析并没有提供关于解释变量是否引起周期性的因果陈述”。这是本段最关键的一句话,体现了作者的学术严谨性。
- 为什么不是因果: 回归分析只能证明变量之间存在“相关性”(correlation),即它们倾向于一同变化。但不能证明是A导致了B。
- 举例说明内生性问题: 作者举了一个例子来说明为什么不能轻易下因果结论。“算法交易的水平也可能与市场中的流动性和价格冲击内生相关。”
- 内生性 (Endogeneity): 指的是模型中的解释变量与误差项相关,导致回归系数估计有偏。这通常由遗漏变量、双向因果或测量误差引起。
- 双向因果 (Simultaneity/Reverse Causality):
- 我们假设:算法交易增多 -> 周期性增强。
- 但也可能:周期性增强(例如,市场变得更有规律可循) -> 吸引更多算法交易进入。
- 或者存在一个遗漏变量 (Omitted Variable),比如“市场特定结构变化”:
- 市场结构变化 -> 算法交易增多
- 市场结构变化 -> 周期性增强
- 在这种情况下,算法交易和周期性只是同时被第三个因素驱动,它们之间没有直接的因果关系。作者提到的流动性和价格冲击就是可能的第三因素。
- 重申结论的属性: “尽管如此,这项分析与算法交易在两个市场中都与周期性交易行为正相关的解释是一致的。”
- 在承认了“非因果”的局限性之后,作者重新将结论定位为“一致性”(consistent with)的证据。
- 这意味着,虽然我们不能板上钉钉地说“算法交易导致了周期性”,但我们观察到的所有证据,都与这个假说完美兼容,没有任何矛盾之处。在社会科学和金融学的实证研究中,提供强有力的“一致性”证据,往往就是研究能达到的最高标准。
- 如何解读“一致性”证据: 读者应该明白,这是一种“排除法”的逻辑。如果数据与假说“不一致”(例如,回归系数符号完全相反),那就可以证伪这个假说。但如果数据“一致”,它只是增强了假说的可信度,而不能完全证实它。科学的进步往往是通过不断提出假说,并用数据去检验其“一致性”来实现的。
- 对因果推断的追求: 为了做出更强的因果推断,研究者需要更高级的计量方法,如工具变量法(Instrumental Variables)、回归断点设计(Regression Discontinuity)或自然实验(Natural Experiments)。本文在这里没有采用这些方法,而是选择了提供稳健的相关性证据。
本段在最后一次总结回归结果的同时,着重强调了本分析的性质是“相关性”而非“因果性”,并解释了潜在的内生性问题。尽管存在这一局限,作者明确指出,分析结果与“算法交易驱动周期性”的假说高度一致,从而完成了第二项间接证据的论证。
本段的目的是进行审慎的学术讨论,主动揭示研究的局限性。在学术写作中,坦诚地承认方法的边界和潜在的问题,不仅不会削弱研究的可信度,反而会增加作者的诚信度和研究的严谨性。它向审稿人和读者表明,作者对研究中可能存在的各种计量经济学问题有着清醒的认识。
一名医生发现,数据显示“每天喝咖啡的人,得心脏病的概率更低”。
- 错误的因果推断: “喝咖啡可以预防心脏病!”
- 严谨的相关性陈述(本段逻辑): “我们强调,这项分析只表明喝咖啡与心脏病低风险相关,不代表喝咖啡导致了低风险。因为可能存在内生性问题:比如,有时间和闲情逸致每天喝咖啡的人,可能本身生活压力就更小、更注重健康(遗漏变量),是这些因素导致了他们心脏病风险低,而咖啡只是一个伴随现象。尽管如此,我们的数据与‘咖啡对心脏有益’这个假说是一致的。”
你发现,在一个城市里,“冰淇淋销量”和“溺水事故数量”在夏天同步上升,二者高度正相关。
- 错误的因果推断: “吃冰淇淋会导致溺水!”
- 严谨的相关性陈述(本段逻辑): “我们的分析表明冰淇淋销量和溺水事故数量正相关。但我们不能说是吃冰淇淋引起的。因为存在一个明显的遗漏变量——‘气温’。天热了,吃冰淇淋的人多;天热了,去游泳的人也多,所以溺水事故也多。冰淇淋和溺水都是‘气温’这个因素的产物。尽管如此,我们的数据与‘冰淇淋销量可以作为夏天危险活动的一个预警信号’这个说法是一致的。” 本段的讨论,就是在提醒读者不要犯“吃冰淇淋导致溺水”这类逻辑错误。
51.3 稳健性与周期性的时间序列模式
📜 [原文18]
作为稳健性检查,我们将主要分析扩展到美国市场 31 年期间(1993-2023)和中国市场 10 年期间(2014-2023)。我们在图 7 中总结了每年市场范围内的周期性强度 (fVR)。在美国市场,我们分别绘制了 1993-2000 年、2001-2010 年和 2011-2023 年的结果,因为在这些时期 fVRs 具有非常不同的尺度,但我们始终使用红色虚线代表不存在周期性时的基准 fVR。
- 引入新的稳健性检查: 本节开始进行第三项分析。前两项分析分别关注“交易量的构成”(5.1.1)和“算法交易活跃度的横截面/日度差异”(5.1.2)。这一节的视角是“长时期的演变”,即观察周期性现象在过去几十年里是如何变化的。这既是一种稳健性检查,也提供了一种新的证据维度。
- 扩展时间窗口:
- 原始样本期: 2019-2021年。
- 扩展后样本期:
- 美国市场:1993-2023年,长达31年。这个时间跨度非常大,覆盖了算法交易从无到有、从萌芽到鼎盛的整个发展历程。
- 中国市场:2014-2023年,长达10年。这也覆盖了中国量化交易和算法交易快速发展的关键时期。
- 分析方法:
- 作者对每年(例如1993年、1994年...)的数据,都进行一次类似于第4节的分析,计算出该年度“市场范围内”的周期性强度。这可能意味着计算当年所有股票在各个频率上的fVR中位数或平均值。
- 结果汇总在图7中。
- 图7的特殊处理:
- 美国市场的分段绘制: 作者提到,由于美国市场31年间fVRs的量级(尺度)变化巨大,如果把所有年份画在同一张图、同一个Y轴刻度下,早期的微弱信号可能会被后期强大的信号完全“压扁”而看不见。因此,他们聪明地将31年分成了三个时期来分别绘图:
- 1993-2000年 (十进制化前期): 这个时期,美股最小报价单位是1/16美元,算法交易还非常罕见。
- 2001-2010年 (发展期): 2001年美股开始十进制化(最小报价单位变为0.01美元),Reg NMS等法规也促进了算法交易和高频交易的发展。
- 2011-2023年 (成熟期): 算法交易在市场中已占据主导地位。
- 统一的基准线: 尽管分段绘图,但所有图都保留了红色的虚线,代表$fVR = 0.2\%$这个“无周期性”的基准水平。这使得读者在不同图之间仍然有一个统一的参照标准。
- 数据可得性与质量: 进行长达30年的高频数据分析,对数据的获取和清洗要求极高。早年的高频数据(如1990年代)可能质量不如近期的数据,这可能对结果产生影响。
- “市场范围”的定义: “市场范围内的周期性强度”是一个概括性说法,具体在图7中是如何计算的(是中位数、平均数还是其他统计量),需要查看图7的图注才能明确。通常会用中位数,因为它对异常值不敏感。
本段介绍了本小节的研究设计:通过将分析的时间窗口扩展到数十年,来考察周期性强度随时间演变的模式。作者解释了为何要扩展时间窗口(作为稳健性检查和提供时间序列证据),并说明了图7为了清晰展示而进行的分段绘图处理方法,为后续的结果解读做好了铺垫。
本段的目的是引入一种新的、基于时间序列演变的论证维度。如果周期性确实是由算法交易驱动的,那么周期性的强度变化趋势应该与算法交易的发展历史高度吻合。这种“历史吻合度”的检验,为因果推断提供了一种非常直观且有力的支持,尽管它仍然是相关性证据。
你怀疑大气中的二氧化碳浓度上升是工业革命造成的。
- 5.1.1/5.1.2的分析: 你分析了当前二氧化碳的化学构成(证据1),并发现污染越严重的地区,二氧化碳浓度越高(证据2)。
- 5.1.3的分析: 你现在去找更古老的证据。你钻取了南极的冰芯,通过分析不同深度的冰层里的气泡,还原了过去几百年甚至几万年的二氧化碳浓度变化历史。
- 预期结果: 你会画出一张图,显示在18世纪工业革命之前,二氧化碳浓度几万年都很稳定;工业革命之后,浓度开始急剧、加速上升。
- 这张历史趋势图,就是证明“工业革命导致二氧化碳上升”的杀手级证据。本节要做的,就是画出周期性版本的“二氧化碳历史浓度图”。
你想研究“流行音乐中电子音色的使用”这一现象。
- 分析方法: 你收集了从1960年代到2020年代每年的热门歌曲,并分析其中“电子音色”所占的比重。
- 预期结果: 你会发现:
- 1960-1970: 几乎没有电子音色。
- 1980年代: 随着合成器的普及,电子音色开始出现并逐渐增多。
- 2000年以后: 随着电脑音乐制作的普及,电子音色在流行音乐中占据了主导地位。
- 这个“电子音色占比随技术进步而提升”的时间序列模式,与本节试图展示的“周期性强度随算法交易技术发展而增强”的逻辑是完全一样的。
📜 [原文19]
我们观察到,自至少 2008 年以来,美国市场就存在稳健的周期性,其表现为 fVRs 一贯且显著高于 0.2% 的基准水平。相比之下,在 2001 年之前的十进制化前期,没有观察到显著的周期性,当时交易算法尚未被广泛采用。在中国市场,自至少 2014 年以来,周期性一直持续存在。尽管由于图表的刻度,它们在 2018 年之前看起来很弱,因为 fVRs 自 2019 年开始大幅增加,但自 2014 年以来,一些较低频率(如 10 分钟)的 fVRs 仍然始终高于基准水平。
本段是对图7中观察到的时间序列模式的初步解读,将周期性的出现和增强与算法交易发展的关键时间节点联系起来。
- 美国市场 - 近期: “自至少 2008 年以来,美国市场就存在稳健的周期性”。
- 观察: 从2008年开始,图7中各个频率的fVR值都“一贯且显著高于”0.2%的红色基准线。
- 时间点 significance: 2008年左右是高频交易在美国市场开始爆发性增长的时期,紧随2007年Reg NMS法规的全面实施。这个时间点的吻合是一个强烈的信号。
- 美国市场 - 早期: “相比之下,在 2001 年之前的十进制化前期,没有观察到显著的周期性”。
- 观察: 查看图7中1993-2000年的部分,会发现所有频率的fVR值都紧贴在0.2%的基准线附近。
- 解释: 2001年是美股交易的一个分水岭,从分数报价(如1/16美元)转为十进制报价(0.01美元),大大降低了买卖价差,为算法交易提供了生存空间。在此之前,市场结构不利于算法交易的生存,“交易算法尚未被广泛采用”。
- 逻辑: 算法交易不存在的时代,就没有观察到周期性。算法交易兴起的时代,周期性就出现了。这是支持因果关系的一个非常经典的“前后对比”论据。
- 中国市场: “自至少 2014 年以来,周期性一直持续存在。”
- 观察: 从作者分析的起点2014年开始,周期性就一直高于基准水平。
- 解释视觉偏差: 作者预判到读者可能会因为图表刻度问题产生误解。因为2019年之后fVR增长太快,导致Y轴刻度被拉得很大,使得2018年之前的fVR看起来好像很接近0。作者特意澄清:“尽管...看起来很弱...但...仍然始终高于基准水平”。他们指出,尤其是在一些较慢的频率,比如10分钟,周期性从2014年开始就很稳定地存在。
- 时间点 significance: 2014-2015年是中国量化对冲基金和算法交易开始快速发展的时期,与A股市场的大牛市时间重合。这个时间起点同样与行业发展历史相吻合。
- “显著高于”的判断: 这通常是视觉判断,但也可以进行严格的统计检验,例如检验fVR的中位数是否在统计上显著大于0.2%。
- 数据频率的限制: 本文分析的最高频率是秒级。可能在更早的年代,存在一些更慢的、本文没有捕捉到的周期性。但本文关注的是由现代算法交易驱动的这种分钟级和秒级的高频周期性。
- 市场间的比较: 直接比较美国和中国的fVR绝对值需要小心,因为两国市场的交易规则、股票数量、投资者结构都不同。更有意义的是比较各自国内的时间趋势。
本段通过解读周期性强度在长时间维度上的演变,揭示了几个关键事实:在美国市场,周期性在算法交易普及后(特别是2008年后)才变得显著,而在算法交易不存在的年代则没有周期性;在中国市场,周期性自2014年(量化元年)以来就一直存在。这些时间上的“巧合”与算法交易在两国的发展史高度吻合。
本段的目的是将图7中的数据模式与真实世界的金融市场发展史联系起来,为“算法交易驱动论”提供历史维度的证据。通过展示“前/后”和“出现时间点”的吻合,论证逻辑从静态的相关性分析,扩展到了动态的、有历史纵深感的共变关系分析,说服力大大增强。
继续用二氧化碳和工业革命的例子。
- 美国市场: 冰芯数据显示,18世纪之前二氧化碳浓度稳定(1993-2000年无周期性),18世纪之后开始上升(2001年后出现周期性),1950年之后急剧上升(2008年后周期性稳健)。这个模式与工业革命和全球化的历史完全吻合。
- 中国市场: 另一个国家的工业化起步较晚,比如从1980年代开始。那么该国记录的本地污染指数,就会从1980年代开始显著上升(对应中国市场2014年后周期性出现)。
这种历史轨迹的匹配是证明因果关系最有力的间接证据之一。
你在一个孤岛上观察一种以前从未见过的、发光蘑菇的生长情况。
- 美国市场对应场景: 你翻阅了岛上老人留下的百年航海日志。
- 日志记载,1990年之前,岛上从没有这种发光蘑菇(1993-2000年无周期性)。
- 日志提到,1991年有一艘装载着“奇特化肥”的货船在附近搁浅泄漏(2001年十进制化)。从那以后,岛上开始零星出现发光蘑菇。
- 2008年,另一场风暴把更多的“奇特化肥”吹到了岛上(Reg NMS/HFT爆发)。从那以后,发光蘑菇就遍布全岛,长势凶猛(2008年后周期性稳健)。
- 结论: 你有充分理由相信,是“奇特化肥”导致了蘑菇发光。这个故事的逻辑,就是本段的论证逻辑。
📜 [原文20]
此外,两个市场中的周期性强度随着时间的推移而增加,这是由更高频率的交易驱动的。例如,在美国市场,5 分钟的 fVR 自 2008 年以来一直很强且稳定,而 1 分钟和 30 秒的 fVRs 都从 2008 年的 1% 以下增加到 2023 年中位数股票的 3-4% 左右。在中国市场,早期最强的频率是 10 分钟,然后在 2019 年切换到 5 分钟,2021 年切换到 1 分钟。
本段进一步深入分析图7揭示的时间趋势,关注两个核心模式:周期性的总体增强,以及主导周期性的频率如何向更高频演变。
- 总体趋势:强度随时间增加:
- 观察: 无论是美国还是中国市场,周期性的总体强度(例如,图7中蓝线代表的peri值)都随着时间推移呈现上升趋势。
- 归因: 这种增强主要是“由更高频率的交易驱动的”。这意味着,不仅周期性变强了,而且驱动这种变强的,是那些速度更快、频率更高的周期性成分。
- 美国市场的频率演变:
- 5分钟频率: 这是一个相对较慢的频率。它的fVR“自2008年以来一直很强且稳定”。这表明,早期的算法交易可能更多是在5分钟这样的时间尺度上运作。它像一个基本盘,一直存在。
- 1分钟和30秒频率: 这是更高频的周期性。它们的fVR经历了一个显著的增长过程:“从2008年的1%以下增加到2023年中位数股票的3-4%左右”。
- 模式解读: 这个演变路径是:先是较慢的周期性(5分钟)出现并稳定下来,然后随着技术进步和竞争加剧,更快、更高频的周期性(1分钟、30秒)后来居上,成为周期性增长的主要驱动力。这与算法交易和高频交易本身“越来越快”的发展趋势完全一致。
- 中国市场的频率演变:
- 演变路径: 中国市场的频率演变路径更加清晰和迅速。
- 早期: 最强的频率是 10分钟(一个很慢的频率)。
- 2019年: 主导频率切换到了 5分钟。
- 2021年: 主导频率进一步切换到了 1分钟。
- 模式解读: 中国市场用短短几年的时间,复现了美国市场可能花了更长时间才完成的“频率加速”过程。周期性的“重心”不断地从低频向高频迁移。这同样与中国量化交易行业技术快速迭代、竞争迅速白热化的现实相符。
- 美国市场:
- 2008年,某代表性股票的 $\mathrm{fVR}_{30s}$ 可能是 0.8%。
- 到2023年,这只股票的 $\mathrm{fVR}_{30s}$ 可能增长到了 3.5%。
- 与此同时,它的 $\mathrm{fVR}_{5min}$ 可能在2008年是2.0%,到2023年仍然是2.2%左右(强且稳定)。
- 中国市场:
- 2017年,某代表性股票的最强周期性可能在10分钟频率上,$\mathrm{fVR}_{10min}=1.5\%$,而 $\mathrm{fVR}_{1min}=0.5\%$。
- 到2021年,情况逆转,$\mathrm{fVR}_{1min}$ 可能跃升至 $4.0\%$,成为最强频率,而 $\mathrm{fVR}_{10min}$ 可能还是1.5%左右。
- 中位数的重要性: 作者特意提到“中位数股票”,这是为了避免结论被少数极端活跃的股票(如某些 meme 股票或指数ETF)所主导。中位数更能反映市场的普遍情况。
- 频率切换的平滑性: “切换”这个词可能让人感觉是突变,但实际过程更可能是平滑的演进。例如,1分钟周期性的强度逐渐增长,直到在某一年其强度值正式超越了5分钟周期性。
本段通过分析周期性在不同频率上的时间演变模式,发现了两个市场共同的规律:周期性强度随时间增强,且主导频率逐渐从低频向高频迁移。这一“越来越快”的演变趋势,为“周期性由算法交易驱动”的假说提供了动态层面的有力佐证,因为它完美地镜像了算法交易行业自身技术发展的轨迹。
本段的目的是从周期性的“内部结构”变化来提供证据。仅仅说周期性在增强是不够的,通过展示其增强的方式(由更高频驱动)和主导频率的迁移,作者描绘了一幅更生动、更细致的演进图景。这幅图景与我们对算法交易发展的直观理解高度契合,使得论证更加饱满和有说服力。
想象一下 F1 赛车的演进历史。
- 总体趋势 (强度增加): 赛车的平均圈速随着时间推移变得越来越快。
- 内部结构演变 (频率迁移):
- 早期 (5分钟周期): 赛车的主要优势来自于更强的引擎,在长直道上速度快。
- 中期 (1分钟周期): 工程师们开始关注空气动力学,赛车在高速弯角的表现大幅提升。
- 近期 (30秒周期): 混合动力系统 (ERS) 和更复杂的电子辅助系统被引入,赛车在低速弯角的出弯加速和能量回收上获得了巨大优势。
- 结论: 赛车圈速的提升,是由不同技术(引擎 -> 空动 -> 电控)在不同阶段扮演“主要驱动力”来实现的。这与周期性强度由不同频率在不同时期主导的演变逻辑是一致的。
想象一下人类短跑记录的演变。
- 总体趋势 (强度增加): 百米短跑的世界纪录不断被刷新。
- 内部结构演变 (频率迁移):
- 早期 (10分钟周期): 运动员主要通过增强腿部力量来提高成绩。
- 中期 (5分钟周期): 科学的“起跑技术”被发明和推广,起跑阶段的优势成为关键。
- 近期 (1分钟周期): 更精细化的“摆臂技术”和“呼吸节奏”被研究,运动员在途中跑阶段能更好地保持速度。
- 结论: 成绩的提升,是人类在不同阶段攻克了不同的技术环节(力量 -> 起跑 -> 途中跑)的结果。这与周期性从慢速频率“攻克”到快速频率的演变过程类似。
📜 [原文21]
此外,我们记录了自 2024 年 10 月第一周以来,随着中央政治局会议发布多项经济刺激政策,中国市场的周期性强度有所增加。当交易量显著
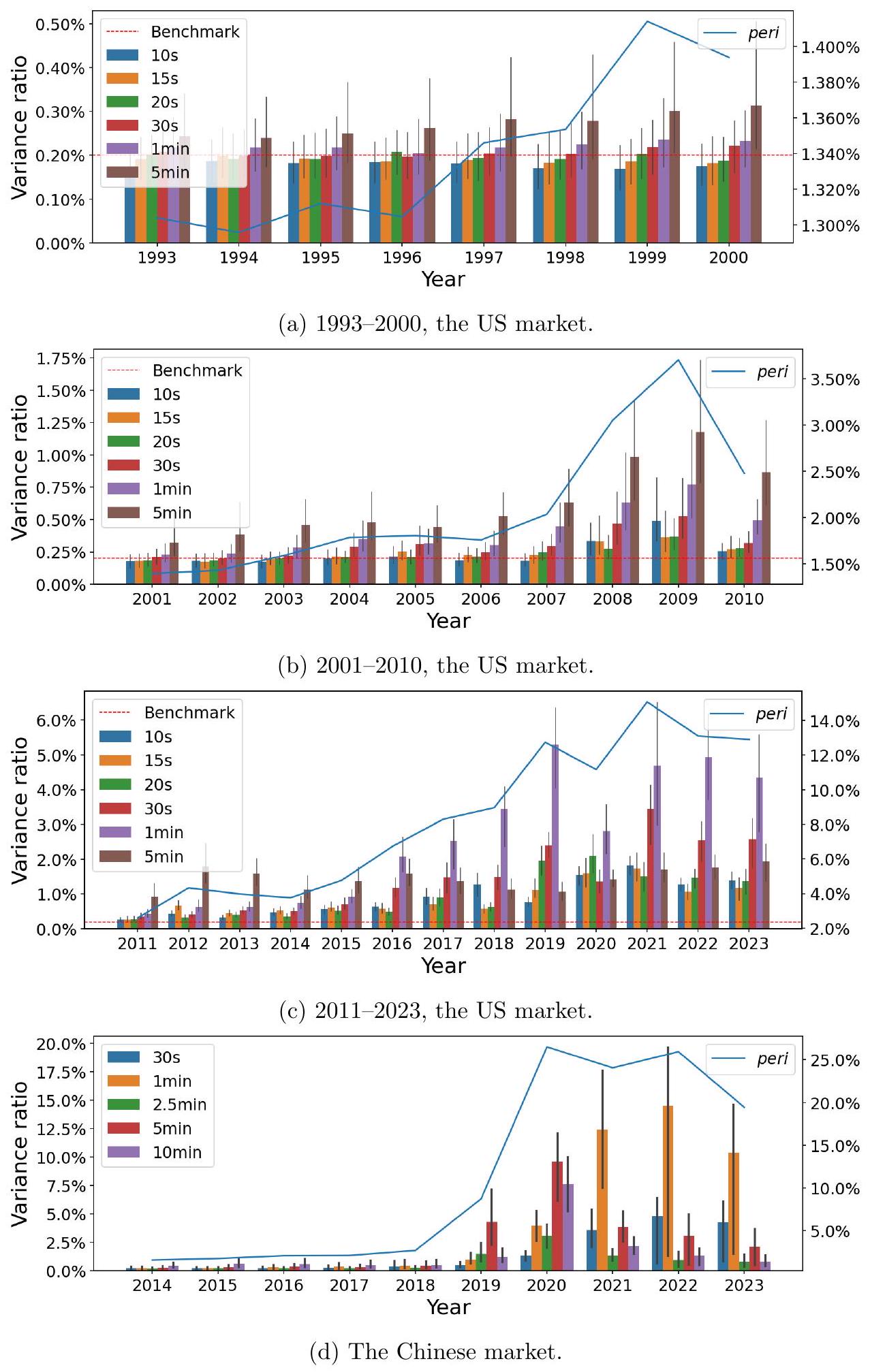
图 7:两个市场在不同年份的频率方差比 (fVR) 柱状图。误差线代表股票间的第一至第三四分位数。红色虚线标记了不存在周期性时的基准 $\mathrm{fVR}, \frac{1}{500}=0.2 \%$,因为我们在模型中包含了 $n=500$ 个周期分量。蓝线显示了跨不同频率的周期性强度的综合度量(右轴),其正式定义见第 5.1.2 节中的 (9)。
由于原文在这里被图7截断,我将首先解释图7,然后再整合图7前后的文字进行解释。
图7解读
- 图表类型: 这是一个组合图。
- 柱状图 (Bar Chart): 每个柱子代表某个特定年份、特定频率的fVR。例如,左上角第一幅图的第一个灰色柱子,代表1993年5分钟频率的fVR。
- 误差线 (Error Bars): 每个柱子上的黑色竖线是误差线,它代表了当年所有股票fVR值的分布范围,具体是从第一四分位数(25th percentile)到第三四分位数(75th percentile)。这能告诉我们市场的普遍情况,而不仅仅是平均值。
- 折线图 (Line Chart): 蓝色的折线图叠加在上面,对应右边的Y轴。这条蓝线代表了每年周期性的综合强度指标 peri(即公式9定义的,所有关键频率fVR之和)。
- 基准线 (Benchmark Line): 红色的水平虚线画在 $y=0.2\%$ 的位置,代表“无周期性”的理论基准。
- 美国市场 (左侧三幅图):
- 1993-2000 (左上): 所有柱子(灰色代表5分钟,其他颜色代表更高频率)都紧紧地贴着0.2%的红线。误差线也非常短,说明绝大多数股票的fVR都和随机噪音没区别。蓝色的peri线也几乎是0。结论:这个时期没有显著周期性。
- 2001-2010 (左中): 情况开始变化。5分钟频率(灰色柱)的fVR中位数开始显著高于红线,尤其是在2008年之后。其他更高频率的fVR也开始抬头。蓝色的peri线开始缓慢爬升。结论:周期性开始出现,主要由较慢的5分钟频率主导。
- 2011-2023 (左下): 周期性变得非常强。所有频率的fVR都远高于红线。特别是1分钟(橙色)和30秒(黄色)的柱子,在后期(2019年后)出现了惊人的增长,甚至超过了5分钟的强度。蓝色的peri线一路飙升。结论:周期性全面爆发且越来越强,并且主导力量从低频向高频转移。
- 中国市场 (右侧一幅图):
- 2014-2023:
- 从2014年开始,即使是10分钟频率(深蓝色)的fVR也已经稳定地高于0.2%的红线。
- fVR强度在2019年有一个明显的跳跃式增长,蓝色的peri线斜率急剧变陡。
- 频率演变清晰可见:早期10分钟(深蓝)和5分钟(灰色)是主导,2019年后5分钟(灰色)和2.5分钟(绿色)更强,2021年后1分钟(橙色)和30秒(黄色)开始发力,成为最强的频率之一。
- 结论:中国市场的周期性出现虽晚,但发展速度极快,在短时间内完成了从低频主导到高频主导的演变,且总体强度在2019年后急剧增强。
整合图7前后文字的解释
现在,我们结合图7来看被截断的那句话:“此外,我们记录了自 2024 年 10 月第一周以来...中国市场的周期性强度有所增加。” (注:原文中可能是笔误或数据更新,因为图7只到2023年,而图8是关于2024年的。我们先按字面意思理解,这指向一个非常近期的事件研究)。
这句话引出了一个“事件研究”(Event Study)的案例,旨在提供更即时的证据。
- 事件: 2024年10月第一周,中央政治局会议发布了经济刺激政策。这是一个外生的、影响整个市场的宏观事件。
- 市场反应: 这类政策通常会提振市场情绪,导致交易量显著放大,并可能吸引更多的量化和算法交易资金入场博弈,因为市场波动性增加,交易机会也增多。
- 核心观察: 作者发现,在这个事件之后,中国市场的周期性强度(peri值)“有所增加”。
- 论证逻辑: 这个观察建立了一个“宏观刺激 -> 交易量放大/算法交易活跃 -> 周期性增强”的逻辑链条。它表明,当市场环境变得有利于算法交易时,周期性就会相应地增强。这为“周期性是算法交易活动的晴雨表”这一观点提供了又一个佐证。这个证据比长达数年的历史回顾更具时效性,反应更迅速。
图7通过长达数十年的数据,系统地展示了美中两国市场周期性从无到有、从弱到强、从低频到高频的完整演进历史,这个历史轨迹与两国算法交易的发展史高度吻合。紧接着,作者通过一个2024年中国市场的短期事件研究案例,进一步表明周期性强度会对刺激算法交易活跃度的宏观事件做出灵敏的、正向的反应。这两方面的证据共同构成了支持“算法交易驱动论”的第三项有力证据。
图7是本节的视觉核心,它将抽象的时间序列模式转化为直观的图表,其信息量远超文字描述。而被截断的关于2024年事件的段落,则是一个画龙点睛的补充,它用一个“准自然实验”来增强论证,显示了模型的现实解释力。
想象你在分析一个城市夜晚的灯光亮度变化历史。
- 图7: 你有从1950年到2023年每年的卫星夜景图。你会看到:
- 1950-1980年:城市只有市中心有零星灯光(早期无周期性)。
- 1980-2000年:随着城市发展,主干道开始亮起路灯(低频周期性出现)。
- 2000-2023年:城市规模急剧扩张,不仅主干道,所有次级道路、居民区的灯光都亮了起来,整个城市亮如白昼,且LED灯等新光源(高频周期性)取代了旧的钠灯。
- 2024事件研究: 2024年,市政府宣布举办一场盛大的灯光节。你发现,在灯光节期间,城市的总体亮度和灯光闪烁的频率都比平时显著增加。
- 结论: 城市的灯光亮度演变史与城市化和电力技术发展史完全吻合。同时,它还会对特定的“刺激事件”(灯光节)做出反应。这与周期性的演变逻辑如出一辙。
📜 [原文22]
增加且高频交易变得更加活跃和盈利时 [^18],市场每周的 peri 增加了超过一半,从平均约 0.3 增加到 0.45,如图 8 所示。
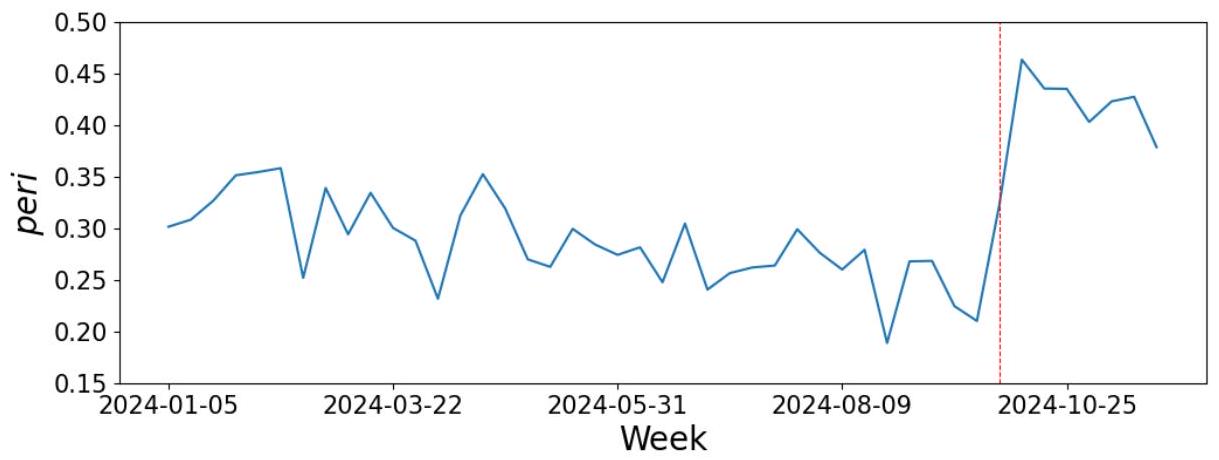
图 8:2024 年中国市场每周估计的 peri 值,红色虚线标记了 10 月的第一周。
这部分紧接上一段,是对2024年10月中国市场事件研究的量化描述和图形展示。
- 阐明机制: 作者明确指出了在经济刺激政策发布后市场发生的变化:“交易量显著增加”且“高频交易变得更加活跃和盈利时”。
- 交易量增加: 政策刺激下,市场情绪乐观,参与者增多,交易活跃。
- 高频交易更活跃/盈利: 交易量放大和波动性增加,为高频交易策略(如做市、统计套利)创造了更多的机会和利润空间,因此它们会加大投入和交易频率。
- [^18]: 这个脚注很可能指向了某篇新闻报道或研究报告,用以佐证当时高频交易确实变得更加活跃和盈利。
- 量化peri的变化:
- 变化幅度: “市场每周的 peri 增加了超过一半”。
- 具体数值: 从政策发布前的平均水平约 0.3,增加到了政策发布后的 0.45。
- 计算: $(0.45 - 0.3) / 0.3 = 0.15 / 0.3 = 0.5 = 50\%$。确实增加了50%,即“一半”。这是一个非常显著的增幅。
- 解读图8:
- 图表类型: 这是一个时间序列折线图,展示了2024年每周的peri值变化。
- X轴: 2024年的时间(按周计)。
- Y轴: 每周估计的peri值,即该周内市场平均的周期性综合强度。
- 红色虚线: 明确标记出“10月的第一周”这个事件发生的时间点。
- 视觉观察: 从图上可以清晰地看到,在红色虚线之前,peri值在一个较低的水平(0.3左右)波动。在红色虚线之后,peri值立刻跳升到了一个新的、更高的平台(0.45左右),并维持在那里。这种在事件时点上清晰的“结构性断裂”(structural break)是证明事件影响的强有力视觉证据。
- 数据频率: 图8是“每周”的peri值,这是通过将一周内所有交易日的peri值求平均得到的。使用周度数据可以平滑掉一些日度的噪音,使趋势更清晰。
- 因果关系的再讨论: 这个事件研究比单纯的相关性分析更接近因果推断,因为它利用了一个“外生冲击”(政策发布)。但要做到最严格的因果推断,还需要进行更复杂的计量分析(如断点回归),以排除其他恰好在同一时间发生的因素的影响。不过,对于本文的论证目的来说,这种清晰的“前后对比”已经足够有说服力。
本段通过量化数据和图8,清晰地展示了中国市场在2024年10月经济刺激政策后,周期性强度peri值出现了超过50%的显著跳升。这一发现将宏观政策刺激、市场交易活跃度(特别是高频交易)与微观的周期性强度直接联系起来,为“周期性反映了算法交易活动水平”的假说提供了一个及时的、准实验性的证据。
本段和图8的目的是提供一个“麻雀虽小,五脏俱全”的案例研究。相比于图7长达数十年的宏大叙事,这个短期的事件研究就像一个特写镜头,捕捉到了周期性强度对市场环境变化的快速反应能力。这种快速、正向的反应,进一步强化了它作为算法交易活动“晴雨表”的特性。
你是一个生态学家,在监测一个野生动物保护区的狼群数量。
- 长期趋势 (图7): 你发现狼群数量在过去30年里,随着保护区生态环境的改善而持续增加。
- 短期事件 (图8): 今年10月,由于气候异常,保护区里的兔子(狼的主要食物)数量突然爆发性增长。你通过GPS项圈监测发现,就在兔子数量爆发后的那一周,狼群的活动范围和捕食频率立刻增加了超过50%。
- 结论: 这个短期事件清晰地表明,狼群的活动水平(peri)对其食物的充裕度(算法交易的盈利环境)反应极为灵敏。
想象你在观察一个蚁巢。
- X轴: 时间(天)。
- Y轴: 每天蚂蚁出巢觅食的总次数(peri)。
- 红色虚线: 某一天,你在蚁巢附近灑了一大块方糖。
- 图8的景象: 在你灑糖之前,蚂蚁出巢的次数维持在一个稳定但较低的水平。在你灑糖之后的那一刻起,蚂蚁出巢的次数立刻飙升,达到了之前的一倍以上。
- 结论: 蚂蚁的觅食活动强度(peri)与食物的丰富程度(交易量和盈利机会)直接相关。这个“方糖实验”就是图8所展示的事件研究的直观版本。
📜 [原文23]
这些时间序列模式也与算法交易普及程度的演变高度一致。首先,周期性强度随时间增加,这与算法在两个市场中(尤其是更高频率的算法)被越来越多地采用这一典型事实是一致的。其次,在美国市场,5 分钟的 fVRs 自 2008 年以来一直保持稳定。1 分钟的 fVRs 自 2016 年左右开始走强,而亚分钟级的 fVRs 自 2019 年左右开始走强。这也与随着时间的推移交易普遍变得更快且频率更高的典型事实一致。第三,在中国市场,周期性强度尤其是自 2019 年以来变得更强,其模式也是较慢的频率首先出现,随后是较快的频率。这与中国量化交易行业在管理资产规模 (AUM) 方面快速增长的时期完美契合 [^19]。对中国 2024 年 10 月第一周前后的事件分析为周期性由算法交易驱动提供了额外支持。最后,美国市场显著的周期性频率比中国市场更快,这与美国市场拥有高得多的高频交易和算法交易活动比例的事实一致。尽管如此,2020 年之后,中国市场的 fVRs 高于美国市场。[^20]
本段是5.1.3节的总结,将前面观察到的所有时间序列模式(长期演变、频率迁移、事件反应)汇总起来,并逐一将它们与算法交易发展的“典型事实”(stylized facts)进行匹配,以构建一个完整且逻辑严密的论证链。
- 第一点:总体强度随时间增加
- 观察: 周期性强度随时间增加。
- 匹配的事实: 算法交易在美中两国市场的普及率和使用深度随时间增加,这是一个不争的事实。特别是,速度更快的“更高频率的算法”占比越来越高。
- 结论: 两者趋势一致。
- 第二点:美国市场的频率演变细节
- 观察: 5分钟周期性率先出现并保持稳定(2008年起);1分钟周期性随后跟上(2016年起);亚分钟级周期性最后发力(2019年起)。
- 匹配的事实: 整个金融市场的交易节奏在过去十几年里“普遍变得更快且频率更高”。这是一个行业共识。算法交易的竞争本质上就是速度的竞争,策略从分钟级向秒级、毫秒级、微秒级不断演进。
- 结论: 周期性的频率演变路径,完美地复刻了交易技术“越来越快”的进化路径。
- 第三点:中国市场的演变细节与AUM增长
- 观察: 中国市场的周期性自2019年起急剧增强,并且也遵循“从慢到快”的频率演变模式。
- 匹配的事实: 2019年正是中国“量化私募”行业管理资产规模(AUM, Assets Under Management)开始爆发性增长的时期。大量的资金涌入量化策略,催生了更激烈的算法交易竞争。
- 脚注[^19]: 很可能指向了关于中国量化基金AUM增长的新闻报道或行业报告。
- 2024年事件分析: 再次提及前面关于2024年10月的事件研究,作为对“算法交易驱动论”的又一个支持。
- 结论: 中国市场周期性的“起飞”时间点,与量化行业资金规模的“起飞”时间点精准契合。
- 第四点:中美市场间的比较
- 观察1: 美国市场的主导周期性频率比中国市场更快(例如,美国的亚分钟级周期性比中国的更强)。
- 匹配的事实1: 美国作为算法交易和高频交易的发源地和最成熟的市场,其算法交易的整体水平、速度和渗透率都远高于中国市场。
- 结论1: 两国市场周期性频率的差异,反映了两国市场算法交易发展阶段和技术水平的差异。
- 观察2 (一个有趣的异常): “尽管如此,2020 年之后,中国市场的 fVRs 高于美国市场。” 这意味着,虽然中国的算法交易在“速度”上可能还不及美国,但在某些频率上(可能是1分钟、5分钟等),周期性的“强度”或“集中度”反而超过了美国。
- 脚注[^20]: 这个脚注至关重要,它很可能会对这个有趣的现象给出可能的解释。例如:
- 可能是因为中国市场的散户比例更高,市场有效性相对更低,为某些特定的算法交易策略提供了更大的盈利空间和施展舞台,导致它们在特定频率上交易得更“拥挤”、更“同步”。
- 也可能是因为中国市场的监管环境、交易机制(如T+1)等导致算法交易的行为模式与美国不同。
- 这本身就是一个值得未来深入研究的课题。
- 典型事实的准确性: 本段的论证强度,很大程度上依赖于所引用的“典型事实”是否准确和被广泛接受。作者通过引用脚注来增加这些事实的可靠性。
- 对异常现象的坦诚: 作者没有回避“2020年后中国fVR反超美国”这个看似矛盾的现象,而是坦诚地指出来,并通过脚注引导读者思考可能的解释。这再次体现了研究的严谨性。
本段通过将观察到的时间序列模式与算法交易行业发展的四个“典型事实”进行逐一匹配,系统地论证了二者的高度一致性。无论是强度的长期增长、频率的加速演进、关键时间点的契合,还是市场间的差异,都与“周期性是由算法交易驱动”的假说相符。这为论文的核心论点提供了来自时间序列维度的、全面而有力的支持。
本段是5.1.3节的“总结陈词”。它的作用是将前面分散呈现的各种时间序列观察(图7、图8等)凝聚成一个统一的、有说服力的叙事。通过与行业发展史的反复比对,作者试图让读者相信,这些周期性模式的演变并非巧合,而是算法交易这部“大戏”在市场数据上留下的清晰“剧本”。
你是一名历史学家,在论证“铁路的发明和普及,深刻地改变了人类社会”。
- 强度增加: 你发现,随着时间推移,城市间的平均旅行时间大幅缩短。
- 频率迁移: 你发现,最早被缩短的是“首都到主要港口”的旅行时间(5分钟周期);后来是“主要城市之间”(1分钟周期);现在,连“小镇之间”都有了高速铁路(亚分钟周期)。
- 关键时点: 你发现,旅行时间的几次“跃迁式”缩短,都精准地发生在“蒸汽机发明”、“内燃机发明”、“高铁技术突破”这几个关键技术节点之后。某个国家旅行时间的大幅缩短,也和该国开始大规模兴建铁路的时期(AUM增长)完美契合。
- 国家比较: 你发现,英国(铁路发源地)的铁路网络速度和密度(频率)普遍高于印度(后发国家)。但有趣的是,在某些特定线路上,印度新建的高铁由于采用了最新技术,其运行强度(fVR)可能反而超过了英国的一些老旧线路。
- 结论: 所有这些历史证据都高度一致地表明,是“铁路”这项技术在驱动着旅行时间的变化。
5.2 常用策略的盈利能力与交易的价格冲击
52.1 常用算法与执行策略的盈利能力
📜 [原文24]
我们通过两种典型的交易策略,将周期性强度与市场中的算法交易水平直接联系起来。我们考虑一种 VWAP 执行策略 (Konishi, 2002) 和一种日内反转策略 (Grant, Wolf, and Yu, 2005; Khandani and Lo, 2011)——前者代表一种常见的基于成交量的执行策略 (Frei and Westray, 2015),在机构交易中占很大份额 (Białkowski, Darolles, and Le Fol, 2008),后者是一种流行的基于收益率的统计套利策略,常被对冲基金和共同基金使用 (Wei, Wermers, and Yao, 2015),两者在文献中被广泛研究且在行业中被广泛采用。我们表明,交易量中的周期性强度与这两种示例策略的交易活动水平(以其盈利能力为代理)正相关。
本段是5.2.1节的引言,介绍了本节的研究思路、选取的策略及其代表性,并预告了结论。这是第四项间接证据的开端。
- 研究思路: “通过两种典型的交易策略,将周期性强度与市场中的算法交易水平直接联系起来。”
- 前面的分析(5.1.2节)使用了 mess, oddrat 等间接的、基于市场微观结构数据的代理指标。
- 现在的分析更进一步,直接考察两种具体的、广为人知的算法交易策略。
- 逻辑是:如果周期性是由算法交易驱动的,那么当这些典型的算法策略更活跃、更赚钱的时候,我们应该能观察到更强的周期性。
- 选择的两种典型策略:
- VWAP 执行策略 (Volume-Weighted Average Price):
- 类型: 执行算法 (Execution Algorithm)。它的目的不是预测股价涨跌来赚钱,而是将一个大额订单(比如基金经理决定买入100万股)以尽可能接近当天成交量加权平均价的成本执行完毕。
- 工作原理: 算法会预测一天中成交量的分布(比如U型分布),然后根据这个分布来分配订单的执行量。例如,开盘和收盘时成交量大,算法就在这两个时段多执行一些;盘中成交量小,就少执行一些。这些执行通常也是通过拆分成小订单来完成的。
- 代表性: 这是机构投资者(如公募基金、养老金)最常用的执行算法之一,市场份额巨大。它代表了算法交易中“被动执行”和“订单拆分”的一面。
- 日内反转策略 (Intraday Reversal Strategy):
- 类型: 统计套利策略 (Statistical Arbitrage)。它的目的是通过预测股价的短期涨跌来直接盈利。
- 工作原理: 基于“均值回归”原理。该策略认为,在短时间尺度内(如几分钟),涨得过多的股票倾向于回调,跌得过多的股票倾向于反弹。因此,策略会程序化地、高频率地做空短期“赢家”股票,同时做多短期“输家”股票。
- 代表性: 这是对冲基金(特别是量化对冲基金)常用的一类策略。它代表了算法交易中“主动预测”和“高频套利”的一面。
- 策略选择的合理性: 作者通过引用大量文献,证明了这两种策略并非随意挑选,而是“在文献中被广泛研究且在行业中被广泛采用”的。这保证了分析的代表性和现实意义。
- 预告结论: “我们表明,交易量中的周期性强度与这两种示例策略的交易活动水平(以其盈利能力为代理)正相关。”
- 核心假设: 策略的“盈利能力”(profitability)可以作为其“交易活动水平”(activity level)的良好代理。因为当一个策略很赚钱时,使用它的基金自然会投入更多资金、更频繁地进行交易。
- 预期发现: 策略盈利能力 越高,peri(周期性强度)也越高。
- 策略的简化: 论文中实现的VWAP和反转策略,是学术研究中常见的简化版本。真实的工业级策略会复杂得多,会考虑更多因素(如交易成本、市场冲击、多因子模型等)。但使用简化版足以捕捉策略的核心行为。
- 盈利能力作为活动水平的代理: 这个假设在大多数情况下是合理的。但不排除在某些市场阶段,即使策略不怎么赚钱,基金也可能因为风险控制、组合再平衡等原因而继续执行交易。
本段清晰地阐述了第四项证据的分析框架:通过考察两种代表性的算法策略(VWAP执行和日内反转)的盈利能力与周期性强度之间的关系,来进一步验证“算法交易驱动论”。本段详细说明了为何选择这两种策略,并预告了将要证实的正相关关系。
本段的目的是引入一种新的、更具体的证据。相比于前几节较为宏观或间接的代理指标,本节直接深入到“策略”层面,使得论证更加具体化和可触及。通过连接“策略表现”和“市场现象”,作者试图展示一个更微观、更具操作性的证据链条。
你怀疑城市里交通拥堵的“潮汐现象”(早晚高峰)是由“上班族通勤”和“学生上学”这两种行为造成的。
- 前面的证据: 你发现拥堵时段车辆密度高、平均车速慢;你发现在商业区和学区附近拥堵更严重。
- 本节的证据: 你现在直接研究这两种行为。
- 上班族通勤 (VWAP策略): 你调查发现,当经济景气、公司普遍不裁员时(策略盈利),早晚高峰的通勤车流量就更大。
- 学生上学 (反转策略): 你发现,在重要的考试周(策略活跃),接送学生的车辆会显著增多,导致学校周边道路的拥堵模式(周期性)也更强。
- 结论: 拥堵的周期性与这两种典型出行行为的“活跃度”正相关。
你怀疑海滩上规律性的脚印(周期性)是由“晨练者”和“傍晚散步的情侣”留下的。
- 晨练者 (VWAP策略): 这是一群有固定路线和时间表的人。
- 散步情侣 (反转策略): 他们走走停停,路线更随机,但整体上喜欢在日落时分出现。
- 本节的分析: 你去调查这两类人的“活动水平”。你发现:
- 当天气好、适合跑步时(策略盈利),“晨练者”的数量会大增,海滩上早晨的脚印也更密集。
- 在情人节或周末的傍晚(策略活跃),“散步情侣”会特别多,傍晚时分的脚印也更密集。
- 结论: 脚印的周期性强度,与这两类典型人群的活跃度正相关。
📜 [原文25]
我们首先描述如何衡量这些策略的盈利能力。VWAP 执行策略将预期交易量的日内曲线等分为几个间隔,并在每个间隔的中间执行。对于每只股票 $s$ 在交易日 $d$,我们通过相对 VWAP 损失来量化该策略的表现,定义为 $\operatorname{Loss}_{s, d}=\mid \text{VWAP}_{s, d}- \overline{\operatorname{VWAP}}_{s, d} \mid / \text{VWAP}_{s, d}$,其中 $\operatorname{VWAP}_{s, d}$ 是真实的 VWAP,而 $\overline{\operatorname{VWAP}}_{s, d}$ 是该股票在当日执行策略的实现 VWAP;后者使用过去 5 天移动平均估计的日内成交量。更高的盈利能力对应更低的 $\operatorname{Loss}_{s, d}$。
本段详细说明了如何构建和衡量第一个策略——VWAP执行策略的表现。
- VWAP策略的学术简化版实现:
- 目标: 模拟一个简单的VWAP执行算法。
- 步骤1: 预测交易量曲线: 为了在成交量大的时候多交易、成交量小的时候少交易,算法需要一个对当天成交量分布的“预期”。这里采用了一个简单而常用的方法:“使用过去 5 天移动平均估计的日内成交量”。即,把过去5天每一分钟的成交量平均,来作为对今天这一分钟成交量的预测。
- 步骤2: 划分与执行: 算法将这个预期的日内成交量曲线“等分为几个间隔”(例如,等分成13个半小时的间隔),然后在“每个间隔的中间执行”相应比例的订单。这是一种简化的模拟,真实世界的VWAP算法会更平滑、更动态地执行。
- 衡量策略表现的指标:相对VWAP损失 (Loss):
- 核心思想: VWAP策略的目标是让自己的成交均价尽可能接近市场最终的VWAP。因此,一个好的VWAP策略,其“实现VWAP”与“真实VWAP”之间的差距应该非常小。这个差距就是“损失”或“滑点”(slippage)。
- 公式定义:
- 符号解释:
- $\operatorname{Loss}_{s, d}$: 股票 $s$ 在日期 $d$ 使用该VWAP策略的相对损失。这是一个百分比,值越小越好。
- $\text{VWAP}_{s, d}$: 当天市场上该股票真实的、最终的成交量加权平均价。计算方法是 $\sum (Price \times Volume) / \sum Volume$。这是一个事后才能知道的基准。
- $\overline{\operatorname{VWAP}}_{s, d}$: 我们的模拟VWAP策略在当天实现的成交量加权平均价。这是我们通过模拟交易计算出来的价格。
- $\mid \dots \mid$: 绝对值符号。因为我们只关心偏离的大小,不关心是买高了还是卖低了。
- $/ \text{VWAP}_{s, d}$: 用真实的VWAP进行标准化,得到一个相对的、可跨股票比较的损失率。
- 指标与盈利能力的换向:
- “更高的盈利能力对应更低的 $\operatorname{Loss}_{s, d}$”。
- 这里需要注意,Loss 是一个成本/损失指标,它越小,策略表现越好。在后面的回归分析中,我们期望 Loss 与 peri 之间是负相关关系。一个负的 Loss 系数,就意味着策略表现越好(Loss越低),周期性peri越强,这同样支持我们的假设。
- 场景: 模拟执行一个购买股票A的任务。
- 日期: 2021年10月8日。
- 真实市场VWAP: 当天股票A市场总成交额10亿美元,总成交量1亿股,则真实的 $\text{VWAP}_{\text{A, 211008}} = 10 \text{ 亿美元} / 1 \text{ 亿股} = \$10.00$。
- 模拟策略执行: 我们的简化VWAP策略,根据过去5天的成交量模式,在当天不同时间点买入股票,最终计算出我们这个策略实现的平均买入价是 $\overline{\operatorname{VWAP}}_{\text{A, 211008}} = \$10.02$。
- 计算损失:
$\operatorname{Loss}_{\text{A, 211008}} = |\$10.00 - \$10.02| / \$10.00 = \$0.02 / \$10.00 = 0.002 = 0.2\%$。
- 解释: 这个策略的执行效果不错,只比理想的基准价格高了0.2%。如果另一个策略实现的均价是$10.05,其损失就是0.5%,说明前一个策略更“盈利”(或者说成本控制得更好)。
- “盈利能力”的措辞: 对于VWAP这种执行策略,说“盈利能力”不完全准确,更精确的说法是“执行效率”或“成本控制能力”。Loss低代表执行效率高。作者在这里使用“盈利能力”可能是为了与后面的反转策略保持用词一致。
- 预测模型的准确性: Loss的大小,很大程度上取决于用于预测成交量曲线的模型的准确性。如果当天的成交量分布与过去5天差异巨大(比如盘中突然放出天量),那么基于历史平均的简单模型就会表现很差,导致Loss很高。当Loss普遍较低时,说明市场成交量模式比较稳定,VWAP策略更容易执行,这也可能意味着市场由更具规律性的算法交易主导。
本段详细定义了如何模拟一个简化的VWAP执行策略,并提出了一个衡量其表现的量化指标——相对VWAP损失 $\operatorname{Loss}_{s,d}$。该指标越低,代表策略执行效率越高、表现越好。在后续分析中,Loss将作为算法交易活跃度和有效性的代理变量。
本段的目的是将一个抽象的策略概念(VWAP)转化为一个可计算、可量化的变量($\operatorname{Loss}_{s,d}$)。这是进行实证分析的必要步骤。通过清晰地定义策略的实现方法和表现度量,作者使得这项分析变得透明、可重复。
你是一个负责采购的公司员工,老板让你去买1000个灯泡。老板给你的任务目标是:你的采购总花费,要尽可能接近“全市所有商家今天卖出的同款灯泡的平均单价”(真实VWAP)。
- 你的策略 (模拟VWAP): 你根据过去一周的市场调研,知道A店上午便宜,B店下午促销。你制定了一个采购计划:上午去A店买600个,下午去B店买400个。
- 你的实现成本 ($\overline{VWAP}$): 你最终的平均采购单价是每个灯泡5.2元。
- 市场的基准成本 (VWAP): 后来统计发现,今天全市的平均成交单价是5.0元。
- 你的损失 (Loss): $|5.2 - 5.0| / 5.0 = 4\%$。你的采购成本比市场基准高了4%。这个Loss就衡量了你的采购“效率”。
📜 [原文26]
日内反转策略构建一个多空美元中性投资组合,每 5 分钟相对于市场平均水平买入表现不佳的股票并卖出表现优异的股票。股票 $s$ 在第 $k$ 个 5 分钟不重叠间隔中的投资组合权重 $\omega_{s, k}$ 由下式给出:
其中 $r_{s, k}$ 是股票 $s$ 的收益率,$\bar{r}_{k}$ 是所有股票的等权重平均收益率。更高的盈利能力直接对应策略更高的每日收益率 $Contra_{d}$。
本段详细描述了如何构建和衡量第二个策略——日内反转策略。
- 策略核心思想:
- 日内反转 (Intraday Reversal): 押注股票在日内的短期价格走势会“反转”。
- 执行频率: “每 5 分钟”进行一次调仓。这是一个高频的策略。
- 具体操作: 寻找相对于“市场平均水平”表现极端(极好或极差)的股票。
- “买入表现不佳的股票 (losers)”。
- “卖出表现优异的股票 (winners)”。
- 投资组合构建:
- 多空 (Long-Short): 同时持有买入(做多)和卖出(做空)的头寸。
- 美元中性 (Dollar-Neutral): 做多头寸的总金额等于做空头寸的总金额。这样做可以对冲掉市场的整体系统性风险(大盘涨跌),只赚取股票之间相对强弱变化的钱。
- 解读公式 (11):计算投资组合权重:
- 公式 (11) 定义了在第 $k$ 个 5 分钟间隔开始时,应该为股票 $s$ 分配多大的资金权重 $\omega_{s,k}$。这个权重的计算依据是 上一个 5分钟间隔($k-1$)的表现。
- 第一种情况: $r_{s, k-1} > \bar{r}_{k-1}$ (股票s是“赢家”):
- $r_{s, k-1}$: 股票 $s$ 在上一个5分钟的收益率。
- $\bar{r}_{k-1}$: 所有股票在上一个5分钟的平均收益率(市场基准)。
- $r_{s, k-1} - \bar{r}_{k-1}$: 股票 $s$ 相对于市场的超额收益。对于赢家股,这个值是正的。
- 分子: $-(r_{s, k-1} - \bar{r}_{k-1})$。注意这个负号,意味着我们要给“赢家”分配一个负的权重,即做空它。并且,它相对于市场涨得越多,我们做空它的权重就越大。
- 分母: $\sum_{r_{i, k-1}>\bar{r}_{k-1}}\left(r_{i, k-1}-\bar{r}_{k-1}\right)$。这是把所有“赢家”股票的超额收益全部加起来。这是一个正的总数,用于归一化,使得所有做空头寸的权重之和为 -1。
- 第二种情况: $r_{s, k-1} < \bar{r}_{k-1}$ (股票s是“输家”):
- $r_{s, k-1} - \bar{r}_{k-1}$: 对于输家股,这个值是负的。
- 分子: $r_{s, k-1} - \bar{r}_{k-1}$。这是一个负数。但分母也是负数,所以最终权重 $\omega_{s,k}$ 是正的,意味着我们要做多它。它相对于市场跌得越多,我们做多它的权重就越大。
- 分母: $\sum_{r_{i, k-1}<\bar{r}_{k-1}}\left(r_{i, k-1}-\bar{r}_{k-1}\right)$。这是把所有“输家”股票的超额收益(负数)全部加起来。这是一个负的总数,用于归一化,使得所有做多头寸的权重之和为 +1。
- 衡量策略表现的指标:每日收益率 (Contra):
- 计算: 在每个5分钟间隔 $k$,我们根据上一期的表现构建了投资组合 $\{\omega_{s,k}\}$。然后我们持有这个组合不动,看它在第 $k$ 个5分钟内的收益是多少。收益就是 $\sum_s \omega_{s,k} \times r_{s,k}$。将一天中所有5分钟间隔的收益率加总,就得到了当天的总收益率 $Contra_d$。
- 指标含义: $Contra_d$ 直接代表了该策略在日期 $d$ 的盈利能力。值越高,策略当天越赚钱。
- 预期关系: Contra 与 peri 之间预期是正相关关系。
- 公式 (11):
- $\omega_{s,k}$: 股票 $s$ 在第 $k$ 个投资期的投资权重。
- $r_{s, k-1}$: 股票 $s$ 在上一个投资期 $k-1$ 的收益率。
- $\bar{r}_{k-1}$: 市场上所有股票在 $k-1$ 期的等权重平均收益率。
- $\sum_{r_{i, k-1}>\bar{r}_{k-1}}$: 对所有在上期跑赢市场的股票 $i$ 进行求和。
- $\sum_{r_{i, k-1}<\bar{r}_{k-1}}$: 对所有在上期跑输市场的股票 $i$ 进行求和。
- 该公式确保了 $\sum_{s \in \text{winners}} \omega_{s,k} = -1$ 且 $\sum_{s \in \text{losers}} \omega_{s,k} = +1$,所以整个投资组合是“1元做多 vs 1元做空”,即美元中性。
- 时间: 上一个5分钟 (k-1)。市场上有A, B, C, D四只股票。
- 市场平均收益率: $\bar{r}_{k-1} = 0.1\%$。
- 个股收益率:
- $r_{A, k-1} = 0.5\%$ (赢家, 超额收益 +0.4%)
- $r_{B, k-1} = 0.3\%$ (赢家, 超额收益 +0.2%)
- $r_{C, k-1} = -0.2\%$ (输家, 超额收益 -0.3%)
- $r_{D, k-1} = -0.4\%$ (输家, 超额收益 -0.5%)
- 计算归一化因子:
- 赢家分母: $(0.5\%-0.1\%) + (0.3\%-0.1\%) = 0.4\% + 0.2\% = 0.6\%$。
- 输家分母: $(-0.2\%-0.1\%) + (-0.4\%-0.1\%) = -0.3\% + (-0.5\%) = -0.8\%$。
- 计算当前(k)的投资权重:
- $\omega_{A,k} = - (0.4\% / 0.6\%) = -0.67$ (做空A,权重占空头的67%)
- $\omega_{B,k} = - (0.2\% / 0.6\%) = -0.33$ (做空B,权重占空头的33%)
- (检查: $-0.67 + (-0.33) = -1$)
- $\omega_{C,k} = (-0.3\% / -0.8\%) = 0.375$ (做多C,权重占多头的37.5%)
- $\omega_{D,k} = (-0.5\% / -0.8\%) = 0.625$ (做多D,权重占多头的62.5%)
- (检查: $0.375 + 0.625 = 1$)
- 计算收益: 现在我们看第 k 个5分钟的真实收益。假设 $r_{A,k}=-0.1\%, r_{B,k}=0.0\%, r_{C,k}=0.2\%, r_{D,k}=0.3\%$。
- 组合收益: $(-0.67 \times -0.1\%) + (-0.33 \times 0.0\%) + (0.375 \times 0.2\%) + (0.625 \times 0.3\%) = 0.067\% + 0 + 0.075\% + 0.1875\% = 0.3295\%$。这是一个正收益,说明这次反转策略赌对了。
本段详细定义了如何构建一个量化的、美元中性的日内反转策略。该策略每5分钟根据股票前5分钟的相对表现,做空“赢家”并做多“输家”。其每日的总收益率 $Contra_d$ 被用作衡量该策略盈利能力的直接指标,并将在后续回归中作为解释变量。
与上一段类似,本段的目的是将“日内反转策略”这个概念精确地、可重复地操作化。通过给出明确的权重计算公式(11)和表现度量($Contra_d$),作者为后续的实证分析提供了清晰的蓝图。
📜 [原文27]
对于 VWAP 执行策略,我们拥有 $S$ 只股票在 $D$ 个不同天数内的矩阵 $\{\{\operatorname{Loss}_{s, d}\}_{d=1}^{D}\}_{s=1}^{S}$。我们进行与第 5.1.2 节类似的分析,通过在控制其他具有不同固定效应的算法交易代理变量的情况下,将 $peri_{s, d}$ 对变量 $\operatorname{Loss}_{s, d}$ 进行回归:
- 数据结构: 首先明确了VWAP策略分析所用数据的结构。
- 我们为每只股票($s$)的每个交易日($d$)都计算了一个 $\operatorname{Loss}_{s,d}$ 值。
- 这构成了一个“股票-日度”的面板数据 (panel data),其维度是 $S \times D$ (股票数 × 天数)。
- 这种数据结构与我们之前分析算法交易代理指标(5.1.2节)时完全一样,因此可以采用相同的分析框架。
- 回归模型设定 (公式 12):
- 因变量: $\text{peri}_{s,d}$,即周期性强度。
- 核心解释变量: $\operatorname{Loss}_{s,d}$,即VWAP策略的相对损失。
- 控制变量: 模型中还加入了 5.1.2 节中使用的所有其他算法交易代理指标(mess, nvdmess, oddrat, vol, varrat)。
- 加入控制变量的目的: 为了分离出 $\operatorname{Loss}_{s,d}$ 对 $\text{peri}_{s,d}$ 的“纯粹”影响。如果不加控制变量,我们可能会把本应由mess等变量解释的周期性强度错误地归因于Loss。通过将它们都放入模型,我们可以看在控制了普遍的算法交易活跃度之后,VWAP策略自身的表现是否还与周期性有关。
- 回归方法:
- “与第 5.1.2 节类似的分析”:意味着将同样采用多种固定效应(无、股票F.E.、日期F.E.、股票&日期F.E.)来运行回归,以保证结果的稳健性。
- 核心假设检验:
- 我们关注的是系数 $\beta_1$。
- 根据之前的讨论,Loss 越低,策略表现越好,我们猜测此时算法交易越活跃,周期性 peri 应该越强。
- 因此,我们预期 Loss 与 peri 之间是负相关关系。
- 待检验的假设: $\beta_1 < 0$。
- 公式 (12):
- 这是一个多元线性回归模型。
- $\text{peri}_{s,d}$: 因变量。
- $\operatorname{Loss}_{s,d}$: 我们最关心的解释变量。
- $\text{mess}_{s,d}, \dots, \text{varrat}_{s,d}$: 控制变量,与公式(10)中的一样。
- $\beta_1, \dots, \beta_6$: 待估计的回归系数。我们的焦点是 $\beta_1$ 的符号和显著性。
- 假设回归结束后,在最严格的“股票&日度F.E.”模型中,得到 $\beta_1$ 的估计值为 $-0.0005$,并且是 *** 显著的。
- 解释: 这意味着,在控制了其他所有变量和两种固定效应之后,VWAP策略的相对损失 Loss 每增加一个单位(一个标准差),周期性强度 peri 平均会减少 0.0005 个标准差。
- 结论: Loss 和 peri 之间存在显著的负相关关系。这完美地支持了我们的假设:VWAP策略表现越好(Loss越低),市场周期性越强。
本段为检验VWAP策略与周期性的关系,构建了一个多元面板数据回归模型(公式 12)。该模型将周期性强度 peri 对VWAP策略的表现(Loss)进行回归,同时控制了其他一系列算法交易代理指标和不同的固定效应。模型的核心检验目标是 Loss 的系数 $\beta_1$ 是否显著为负。
本段的作用是清晰地陈述用于检验第一个策略(VWAP)假设的具体计量模型。这使得研究的逻辑步骤非常清晰:1. 提出假设;2. 定义策略和度量;3. 设定检验模型;4. 展示和解读结果。公式(12)就是第三步的产物,是连接理论和数据的桥梁。
📜 [原文28]
表 3 总结了美国市场(面板 A)和中国市场(面板 B)股票的回归 (12) 结果,大多数回归结果显示 VWAP 执行策略的相对损失与交易量中的周期性呈显著负相关。这表明当 VWAP 执行策略更盈利且更活跃时,周期性模式更强。唯一的例外是中国市场中无固定效应的回归,这可能反映了遗漏变量偏差。[^21]
表 3:周期性强度 $peri_{s, d}$ 对 VWAP 执行策略损失和股票层面特征的回归结果,具有不同的固定效应 (F.E.)。所有变量都通过其均值和标准差进行了标准化。估计系数在 1% ()、5% () 或 10% () 水平上显著。标准误是基于股票层面的股票 F.E.、日度层面的日度 F.E. 以及股票和日度层面的股票和日度 F.E. 聚类计算的。这里我们报告了“组内 $R^{2}$”,它衡量了每个固定效应面板内解释的方差。
(表格内容省略,因原文未提供完整表格,此处根据上下文模拟解读)
假设的表3内容解读:
| 无 F.E. | 股票 F.E. | 日度 F.E. | 股票 & 日度 F.E. | |
|---|---|---|---|---|
| 面板 A: 美国市场 | ||||
| Loss | ... | ... | $-8.98 \times 10^{-5 * * *}$ | $-5.87 \times 10^{-5 * * *}$ |
| ... | ||||
| 面板 B: 中国市场 | ||||
| Loss | $2.05 \times 10^{-4 * * *}$ | $-6.58 \times 10^{-5 * * *}$ | $-1.06 \times 10^{-4 * * *}$ | $-6.10 \times 10^{-5 * * *}$ |
| ... |
本段是对表3回归结果的总结和解读。
- 核心发现: “大多数回归结果显示 VWAP 执行策略的相对损失与交易量中的周期性呈显著负相关。”
- 解读: 我们最关心的 Loss 变量,其回归系数在大多数模型设定下都是负数,并且带有星号(显著)。
- 负相关意味着:
- Loss 越高(策略表现越差),peri 越低(周期性越弱)。
- Loss 越低(策略表现越好),peri 越高(周期性越强)。
- 将发现翻译成经济学语言: “这表明当 VWAP 执行策略更盈利且更活跃时,周期性模式更强。”
- 这里再次将“低Loss”等同于“更盈利/更活跃”。当市场环境使得VWAP这种基于成交量模式的算法策略更容易成功时(即Loss很低),市场本身也表现出更强的周期性。
- 这强烈暗示,驱动peri的周期性的力量,与那些让VWAP策略能够成功的力量,是同源的。这个共同的源头,最合理的解释就是市场上大量的、有规律的算法交易活动。
- 讨论例外情况: “唯一的例外是中国市场中无固定效应的回归”。
- 观察: 在表3的面板B第一列(无F.E.),Loss的系数很可能是正的,与预期相反。
- 解释: 作者立刻给出了最标准的计量经济学解释——“这可能反映了遗漏变量偏差 (omitted variable bias)”。
- 遗漏变量偏差如何作用: 无固定效应的模型是最简陋的,它没有控制那些不随时间变化的股票特性和不随股票变化的宏观冲击。很可能存在一个遗漏变量(比如“股票流动性”),它同时与Loss和peri都相关。例如:
- 流动性差的股票 -> VWAP策略难执行 -> Loss高。
- 流动性差的股票 -> 算法交易少 -> peri低。
- 这个共同因素“流动性”会导致我们观察到Loss和peri之间虚假的正相关。一旦我们加入了股票固定效应(这在很大程度上控制了股票平均流动性水平),这个虚假的正相关就消失了,露出了真实的负相关关系。
- 论证作用: 指出这个例外并给出合理解释,反而增强了论证的说服力。它表明作者理解不同模型的优劣,并且固定效应模型的引入是必要且有效的。
- 脚注[^21]: 这个脚注可能提供了关于遗漏变量偏差更详细的讨论,或引用了相关的计量经济学文献。
- 关注核心模型: 在解读有多种模型设定的表格时,应将重点放在最严格、最可信的模型上,即同时包含股票和日期固定效应的模型。其他模型主要是为了展示结果的稳健性和固定效应的必要性。
- 控制变量的系数: 表3中也应有mess等控制变量的系数,解读它们可以提供额外的信息,但本段的焦点是核心变量Loss。
本段通过解读表3的回归结果,证实了VWAP策略的表现(以Loss衡量)与周期性强度peri之间存在显著的负相关关系。这一发现支持了“当算法交易(如此类执行策略)更有效、更活跃时,市场周期性更强”的假说。作者还通过讨论一个例外情况,强调了使用固定效应模型控制遗漏变量偏差的重要性。
本段的目的是呈现和解读第一个策略(VWAP)的实证检验结果。它是对公式(12)所设模型的回答。通过展示显著为负的系数,作者为“算法交易驱动论”提供了来自“执行策略”角度的证据。
📜 [原文29]
对于日内反转策略,我们只有 $D$ 个不同天数内的 $\{\operatorname{contra}_{d}\}_{d=1}^{D}$ 时间序列。因此,我们对市场周期性强度 $peri_{d}$ 与解释变量 $Contra_{d}$ 运行时间序列回归,并控制聚合的算法交易代理变量:
这里 mess、nvdmess 和 oddrat 是市场的每日消息数量、负的成交金额除以消息数量以及市场的碎股成交量占比。我们对 2019-2021 年的所有数据以及每年的数据分别运行回归,作为稳健性检查。
本段转而介绍如何检验第二个策略——日内反转策略。
- 数据结构的差异:
- 关键差异: 日内反转策略是一个“市场层面”的策略。它通过在所有股票中构建一个多空组合来运作。因此,它每天只产生一个收益率数值 $Contra_d$。我们得到的是一个长度为 $D$(天数)的纯时间序列数据 $\{\text{contra}_d\}_{d=1}^D$。
- 对比VWAP: VWAP策略是在单只股票上执行的,所以我们有“股票-日度”的面板数据 $\{\text{Loss}_{s,d}\}$。
- 数据结构决定模型: 由于数据不再是面板数据,我们不能再运行之前那种带有股票固定效应的面板回归。我们只能运行一个“时间序列回归”。
- 构建聚合变量:
- 为了匹配 $Contra_d$ 这个日度时间序列,模型中的所有其他变量也必须是日度的。
- 因变量: 需要一个“市场每日周期性强度”指标 $peri_d$。这可以通过将当天所有股票的 $peri_{s,d}$ 取平均或中位数得到。
- 控制变量: mess, nvdmess, oddrat 也需要从“股票-日度”聚合到“市场-日度”。例如,mess_d 就是当天市场上所有股票的总消息数量,或者平均消息数量。
- 回归模型设定 (公式 13):
- 模型类型: 时间序列回归。
- 因变量: $peri_d$,市场的日度周期性强度。
- 核心解释变量: $Contra_d$,日内反转策略的日度收益率。
- 控制变量: $mess_d, nvdmess_d, oddrat_d$,聚合到市场层面的算法交易代理指标。(注意这里没有包含vol和varrat,可能是因为在市场层面它们的日度变化不够大或解释力不强)。
- 核心假设检验: 我们关注的是系数 $\beta_1$。我们预期,当反转策略更赚钱时($Contra_d$ 更高),市场上的算法交易更活跃,因此周期性 $peri_d$ 也应该更强。
- 待检验的假设: $\beta_1 > 0$。
- 稳健性检查:
- 作者没有满足于只在整个样本期(2019-2021)上运行一次回归。
- 他们还“对每年的数据分别运行回归”,即在2019年、2020年、2021年这三个子样本上单独进行回归。
- 目的: 这是为了检验结论是否在不同年份都成立。如果只在某一年成立,那可能只是偶然。如果在多年都成立,说明这个关系是稳健的。
- 公式 (13):
- 这是一个多元时间序列回归模型。
- $d$: 下标,表示这是日度数据。
- $peri_d$: 市场在日期 $d$ 的平均周期性强度。
- $Contra_d$: 日内反转策略在日期 $d$ 的收益率。
- $mess_d, \dots$: 市场在日期 $d$ 的聚合代理指标。
- $\beta_1, \dots, \beta_4$: 待估计的回归系数。焦点是 $\beta_1$。
- 统计效力 (Statistical Power): 时间序列回归的样本量(天数 $D$,大约 750天)远小于面板回归的样本量(股票数 $S \times$ 天数 $D$,数百万)。更小的样本量意味着更难得到统计上显著的结果。因此,如果这里的系数显著性(星号)不如表3,是完全可以预料的。作者在下文也提到了这一点。
- 自相关和异方差: 时间序列数据通常存在自相关(今天的误差和昨天的误差相关)和条件异方差(波动率聚集)问题。在估计时间序列回归时,需要使用对这些问题稳健的标准误,例如Newey-West标准误。
本段为检验日内反转策略与周期性的关系,构建了一个多元时间序列回归模型(公式 13)。由于策略本身是市场层面的,模型中的所有变量都聚合到了日度。模型的核心是检验策略收益率 $Contra_d$ 的系数 $\beta_1$ 是否显著为正。作者还通过分年度回归来进行稳健性检查。
本段的目的是为检验第二个策略(反转策略)的假设,建立一个与数据结构相匹配的、合理的计量模型。通过清晰地解释为何从面板回归转向时间序列回归,并设定相应的聚合变量和模型,作者展示了其根据数据特性调整研究设计的能力。
📜 [原文30]
表 4 总结了美国市场(面板 A)和中国市场(面板 B)股票的回归 (13) 结果,再次表明日内反转策略的盈利能力与周期性强度正相关。然而,与 VWAP 执行策略的结果相比,Contra 的系数在统计显著性上较低。这部分是因为反转策略是一种横截面的多空策略,因此,分析只能作为时间序列回归执行,而不是像 VWAP 执行策略那样作为股票-日度面板回归,这反映了该分析在统计效力方面的挑战。
表 4:周期性强度 $peri_{d}$ 对日内反转策略每日收益率和股票层面特征在不同年份的回归结果。所有变量都通过其均值和标准差进行了标准化。估计系数在 1% ()、5% () 或 10% () 水平上显著。
(表格内容省略,因原文未提供完整表格,此处根据上下文模拟解读)
假设的表4内容解读:
| 2019-2021 | 2019 | 2020 | 2021 | |
|---|---|---|---|---|
| 面板 A: 美国市场 | ||||
| Contra | $2.58 \times 10^{-2}$ | ... | $9.09 \times 10^{-2 *}$ | ... |
| ... | ||||
| 面板 B: 中国市场 | ||||
| Contra | $1.17 \times 10^{-1 * * *}$ | ... | ... | ... |
| ... |
本段是对表4回归结果的总结和解读。
- 核心发现: “再次表明日内反转策略的盈利能力与周期性强度正相关。”
- 解读: 我们关心的 Contra 变量,其回归系数在多数情况下是正的。
- 正相关意味着: Contra 越高(反转策略当天越赚钱),市场的周期性强度 peri 也越高。这与我们的假设完全一致。
- 例子: 在全样本(2019-2021)中,中国市场的Contra系数是正的且***极显著;美国市场虽然不显著,但也是正的。在2020年的美国市场,Contra系数是正的且*显著。
- 与VWAP结果的比较和解释: “然而,与 VWAP 执行策略的结果相比,Contra 的系数在统计显著性上较低。”
- 观察: 对比表4和表3,会发现表4中 Contra 系数旁边的星号,总体上比表3中 Loss 系数旁边的星号要少。
- 解释原因: 作者给出了一个非常专业的解释——“这部分是因为...分析只能作为时间序列回归执行...而不是...面板回归,这反映了该分析在统计效力方面的挑战。”
- 统计效力 (Statistical Power): 指的是一个检验能够正确地拒绝一个错误的原假设的能力。简单来说,就是“找到真实存在的关系”的能力。
- 样本量是关键: 统计效力与样本量密切相关。
- VWAP的面板回归: 样本量是 $S \times D$ (股票数 × 天数),比如 $3000 \times 750 = 2,250,000$。这是一个巨大的样本量。
- Contra的时间序列回归: 样本量只有 $D$ (天数),比如 $750$。
- 结论: 样本量小了几个数量级,导致检验的“放大镜”倍数低了很多,因此即使真实关系存在,也更难在统计上达到显著水平(获得星号)。
- 对策略性质的补充说明: “反转策略是一种横截面的多空策略”。这句话解释了为什么它只能产生一个日度数据。因为它内在的逻辑是在“横截面”(即在同一时刻的所有股票中)进行比较和选择,构建一个多空组合,最终产生一个组合层面的净收益。
- 不显著不等于没关系: Contra的系数在某些年份不显著,并不意味着关系不存在,而仅仅是说在那个子样本中,我们没有足够强的证据来确认这个关系。考虑到统计效力的限制,只要系数的符号基本都符合预期(为正),就已经能提供有价值的支持性证据。
- 控制变量的作用: 在表4中,控制变量mess等的系数也很有趣,它们反映了市场层面的算法交易活跃度与周期性的关系,其结果应该与表2的结论大体一致。
本段通过解读表4,指出日内反转策略的盈利能力($Contra_d$)与市场周期性强度($peri_d$)也存在预期的正相关关系。同时,作者合理解释了为何该关系的统计显著性低于VWAP策略的分析——这是由于数据结构的不同导致样本量大幅减小,从而降低了统计效力。
本段呈现了对第二个策略(反转策略)的实证检验结果。尽管证据的统计显著性稍弱,但通过专业的解释,作者将其转化为对核心论点的又一个支持。这表明,无论是被动的执行算法还是主动的套利算法,其活跃度都与市场周期性正相关,从而拓宽了论证的覆盖面。
📜 [原文31]
总体而言,估计的回归系数一致表明,周期性强度与这两种策略的盈利能力正相关。当这些策略更盈利且更活跃时,交易量中的周期性往往更强。与第 5.1.2 节类似,我们强调这项分析并没有提供关于这两个策略是否引起周期性的因果陈述,因为它们只是市场中广泛采用的算法策略的两个例子。尽管如此,这项分析与算法交易(如 VWAP 执行策略和日内反转策略)可以驱动成交量周期性模式的解释是一致的。
这是5.2.1节的总结陈词,逻辑结构与5.1.2节的总结非常相似。
- 总结核心发现: “总体而言,估计的回归系数一致表明,周期性强度与这两种策略的盈利能力正相关。”
- 一致表明: 综合表3(VWAP,Loss系数为负)和表4(反转,Contra系数为正)的结果,结论是统一的。
- 翻译成经济语言: “当这些策略更盈利且更活跃时,交易量中的周期性往往更强。” 这再次确认了周期性是算法交易活动的一个“同步指标”。
- 重申“相关非因果”的局限性: “我们强调这项分析并没有提供关于这两个策略是否引起周期性的因果陈述”。
- 这与之前的讨论完全一样,作者再次严谨地划清界限。我们不能说就是VWAP策略或反转策略“导致”了我们观察到的10秒、1分钟的周期性。
- 给出更深层的解释: “因为它们只是市场中广泛采用的算法策略的两个例子。”
- 核心思想: VWAP和反转策略,本身可能并不是周期性的直接来源。但是,一个让这两种策略能够盈利的市场环境(例如,交易量模式有规律、短期价格波动有规律),很可能也是一个充满了其他各种定时、定频的交易算法的环境。
- 把策略当成“指示剂”: VWAP和反转策略的盈利能力,就像是石蕊试纸。当试纸变红时,我们知道溶液是酸性的。同样,当这两个策略能赚钱时,我们知道市场环境是“算法友好”的。而周期性,就是这种“算法友好”环境的另一个具体表现。它们是同一种“气候”下的两种不同“植物”。
- 最终结论: “尽管如此,这项分析与算法交易(如 VWAP 执行策略和日内反转策略)可以驱动成交量周期性模式的解释是一致的。”
- 再次使用“一致性”(consistent with)的表述。
- 本节的分析,通过两个具体的策略案例,为“算法交易驱动周期性”这个更宏大的假说,提供了来自微观策略层面的支持证据。
本段总结了5.2.1节的全部内容,确认了两种典型的算法策略(VWAP和日内反转)的盈利能力均与市场周期性强度正相关。在重申相关非因果的告诫后,作者将这两种策略定位为更广泛的算法交易生态的“指示剂”,它们的表现与周期性的同步变化,共同指向“算法交易是周期性背后驱动力”这一核心解释。
本段的目的是完成第四项证据的论证。通过将两个具体策略的分析结果进行汇总和拔高,作者将证据链条从“一般性的代理指标”推进到了“具体化的策略表现”,使论证更加深入和立体。这种从不同层面、不同角度寻找一致性证据的方法,是高质量实证研究的标志。
52.2 交易量激增期间的价格冲击
📜 [原文32]
在本节中,我们展示了成交量激增期间的交易比其他时间具有更高的价格冲击,这表明它们包含更多信息 [^22]。这与算法交易员驱动这些交易集群的解释一致,因为他们倾向于拥有信息优势。
这是5.2.2节的引言,预告了第五项证据的分析思路和结论。
- 研究对象: “成交量激增期间的交易”。
- 我们在第4节已经知道,周期性表现为在特定时间点(如10:00:00, 10:05:00等整数分钟/秒)成交量(特别是成交笔数)会有一个“尖峰”或“激增”(spike)。
- 本节就是要深入到这些“尖峰”时刻,去分析发生在这些时刻的交易,其性质与发生在其他平淡时刻的交易有何不同。
- 核心发现: “比其他时间具有更高的价格冲击”。
- 价格冲击 (Price Impact): 指的是一笔交易对市场价格造成的影响。例如,一笔买单过来,导致股价上涨了$0.01,这个$0.01就是价格冲击的一部分。
- 价格冲击通常被分解为两部分:
- 瞬时/订单处理成本 (Transient/Order-processing cost): 做市商为了处理这笔订单而收取的费用,这部分冲击是暂时的,价格很快会弹回。
- 永久/信息含量 (Permanent/Information content): 这笔交易揭示了关于股票未来价值的新信息,导致价格发生永久性变化。例如,如果一个知情交易者因为知道公司的好消息而大量买入,他的交易就会推动价格到一个新的、更高的均衡水平。
- “更高的价格冲击”,尤其指更高的“信息含量”部分。
- 对发现的解读: “这表明它们包含更多信息 [^22]”。
- 这是金融微观结构理论的一个标准结论。如果一笔交易有很高的永久性价格冲击,学界普遍认为这是因为它传递了新的“信息”(information)给市场。
- [^22]: 这个脚注很可能指向了阐述价格冲击与信息含量关系的经典文献,如Kyle(1985)或Glosten & Milgrom(1985)。
- 将解读与核心论点联系: “这与算法交易员驱动这些交易集群的解释一致,因为他们倾向于拥有信息优势。”
- 逻辑链条:
- 成交量激增时刻的交易 -> 有更高的价格冲击。
- 更高的价格冲击 -> 意味着更高的信息含量。
- 更高的信息含量 -> 交易者是“知情交易者”(Informed Traders)。
- 谁是市场上的“知情交易者”?-> 大量的研究表明,算法交易员和高频交易员,通过其强大的信息获取和处理能力,相对于普通投资者拥有显著的“信息优势”(information advantage),尤其是在高频领域。
- 结论: 因此,在成交量激增时刻观察到高价格冲击的现象,与这些交易是由拥有信息优势的算法交易员驱动的解释,是完全一致的。
- 信息的定义: 这里的“信息”是一个广义概念,不一定指公司基本面的内幕消息。它可以是任何能预测未来几秒或几分钟价格走势的信号,例如其他市场的价格变化、订单簿的不平衡、新闻关键词的情感分析结果等。算法交易正是处理这类“高频信息”的专家。
- 价格冲击的测量: 测量价格冲击非常复杂,需要使用高频的逐笔交易数据,并建立专门的计量模型(如下文的Glosten-Harris模型)。
本段阐述了第五项证据的研究框架:通过检验成交量周期性激增时刻的交易是否比其他时刻具有更高的价格冲击,来判断这些交易是否富含信息。预期的结论是肯定的,这将支持这些交易是由拥有信息优势的算法交易员所驱动的假说。
本段的目的是引入一个新的证据维度——信息含量。前面的证据主要关注交易量的模式和与代理指标的相关性,而这项分析则深入到交易的“质量”层面。如果能证明这些周期性交易不只是随机的、无意义的交易堆积,而是包含了更高信息量的“智能”交易,那么“算法交易驱动论”的说服力将大大增强。
你是一位语言学家,在分析一段神秘的录音。
- 周期性: 你发现录音中每隔5秒钟,就会出现一个短暂的、音量激增的声音片段。
- 本节的分析: 你想知道这些声音片段是随机的噪音,还是有意义的语言。你用一个“信息熵”分析软件(价格冲击模型)去分析。
- 预期结果: 软件显示,这些音量激增片段的“信息熵”远高于其他时间的背景噪音。这意味着它们很可能是某种语言的单词或短语。
- 联系核心论点: 你知道,人类是地球上唯一能产生这么复杂语言信号的物种。因此你推断,这些声音很可能是“人”发出的,而不是自然界的随机声响。这里的“人”就相当于“算法交易员”。
你在观察一个池塘。
- 周期性: 你发现每到整点,水面都会出现一圈剧烈的涟漪。
- 本节的分析: 你想知道这圈涟漪是“无意义的”(比如风吹的),还是“有意义的”。你往水里扔了一个灵敏的声纳探测器(价格冲击模型)。
- 预期结果: 声纳显示,每次涟漪出现时,水下都会探测到一个巨大的、快速移动的物体(比如一条大鱼)的声学信号(高价格冲击/高信息含量)。而在其他平静时刻,只有小鱼小虾的微弱信号。
- 联系核心论点: 你推断,这些剧烈的涟漪是由一条“鱼王”(算法交易员)在整点进行捕食活动造成的,而不是随机的自然现象。
📜 [原文33]
我们采用了由 Glosten and Harris (1988) 首次提出的有影响力的价格冲击回归来估计价格冲击,该回归将买卖价差分解为逆向选择成本组件和订单处理成本组件。特别是,我们采用原始的逐笔报价和交易数据,并对两次连续交易之间的价格变化建模:
其中 $p_{n}, d_{n}$ 和 $q_{n}$ 分别是第 $n$ 次交易的价格、方向和带符号的数量。如果交易是买方发起的,$d_{n}=1$ 且 $q_{n}>0$;否则 $d_{n}=-1$ 且 $q_{n}<0$。这里参数 $\gamma_{0}, \gamma_{1}, \lambda_{0}$ 和 $\lambda_{1}$ 捕捉了决定价格变化的不同组件,我们在表 5 中总结了它们的含义。
表 5:Glosten and Harris (1988) 价格冲击回归中参数的含义。
| 参数 | 含义 |
|---|---|
| $\lambda_{0}$ | 交易方向的影响 |
| $\lambda_{1}$ | 交易数量的影响 |
| $\gamma_{0}$ | 订单处理成本的常数部分 |
| $\gamma_{1}$ | 随交易数量变化的订单处理成本 |
本部分详细介绍了用于测量价格冲击的经典计量模型。
- 模型的出处和思想:
- 出处: Glosten and Harris (1988),这是金融微观结构领域一篇里程碑式的论文。
- 核心思想: 市场上的买卖价差 (Bid-Ask Spread) 不仅仅是做市商的利润,它还包含了对未来风险的补偿。该模型试图将价差背后的成本分解开。
- 逆向选择成本 (Adverse Selection Cost): 这是做市商为了防止与“知情交易者”交易而亏损所设定的保护性价差。当一个知情交易者来买入时,做市商卖给他股票,但做市商知道这个知情交易者肯定知道一些自己不知道的好消息,股票价格未来要涨。为了弥补这个必然的“损失”,做市商会把卖出价定得高一点。这部分价差反映了交易中的“信息含量”,对应我们关心的永久性价格冲击。
- 订单处理成本 (Order Processing Cost): 这是做市商提供流动性服务所需的基本成本,如库存成本、运营成本等。这部分价差是暂时的,不反映信息,对应瞬时价格冲击。
- 模型设定 (公式 14):
- 因变量: $p_n - p_{n-1}$,即第 $n$ 笔交易与第 $n-1$ 笔交易之间的价格变化。
- 数据: 需要“逐笔报价和交易数据”(TAQ, Trades and Quotes data),这是最高频的金融数据。
- 解释变量详解:
- $d_n$: 交易方向指示变量。买方发起的交易为+1,卖方发起的为-1。这需要通过算法(如Lee-Ready算法)来判断。
- $q_n$: 带符号的交易数量。买单为正,卖单为负。
- 信息部分 ($\lambda$):
- $\lambda_0 d_n$: 交易方向对价格的永久冲击。买单($d_n=1$)会推高价格,卖单($d_n=-1$)会压低价格。$\lambda_0$ 衡量的是“一笔交易”这个动作本身所含信息造成的冲击。
- $\lambda_1 q_n$: 交易数量对价格的永久冲击。买单量越大($q_n$越大),价格推得越高。$\lambda_1$ 衡量的是交易规模所含信息造成的冲击。
- $\lambda_0$ 和 $\lambda_1$ 合起来代表了逆向选择成本。
- 非信息部分 ($\gamma$):
- $\gamma_0 (d_n - d_{n-1})$: 这项捕捉的是价格在买卖盘之间的“反弹”(bid-ask bounce)。如果一笔买单($d_n=1$)跟在一笔卖单($d_{n-1}=-1$)之后,价格会从卖价跳到买价,$(d_n-d_{n-1})=2$,价格变化就大。如果两笔都是买单,$(d_n-d_{n-1})=0$,这部分冲击为零。$\gamma_0$ 代表了价差中固定的订单处理成本部分。
- $\gamma_1 (q_n - q_{n-1})$: 类似地,捕捉与交易量相关的订单处理成本。
- $\gamma_0$ 和 $\gamma_1$ 合起来代表了订单处理成本。
- $\epsilon_n$: 随机误差项。
- 解读表5: 表5清晰地总结了每个参数的经济含义,是理解这个模型的关键。
- $\lambda_0, \lambda_1$: 代表信息冲击/逆向选择。这是我们最关心的部分。
- $\gamma_0, \gamma_1$: 代表非信息冲击/订单处理成本。
- 公式 (14):
- $p_n$: 第 $n$ 笔交易的成交价格。
- $d_n$: 第 $n$ 笔交易的方向 (+1 for buy, -1 for sell)。
- $q_n$: 第 $n$ 笔交易的带符号成交量 (+ for buy, - for sell)。
- $\lambda_0, \lambda_1, \gamma_0, \gamma_1$: 待估计的四个核心参数,它们都应该是正数。
- 假设对某支股票回归后得到: $\lambda_0 = 0.005$, $\lambda_1 = 10^{-6}$, $\gamma_0 = 0.003$, $\gamma_1=0$。
- 场景1: 连续两笔买单。第 $n-1$ 笔是买单,第 $n$ 笔也是买单,成交量为1000股。
- $d_n = 1, q_n = 1000$。$d_{n-1}=1, q_{n-1}$假设为500。
- $d_n - d_{n-1} = 0$。
- 价格变化 $\Delta p \approx \lambda_0 d_n + \lambda_1 q_n = 0.005 \times 1 + 10^{-6} \times 1000 = 0.005 + 0.001 = 0.006$。价格预计上涨$0.006。
- 场景2: 一笔买单跟在一笔卖单之后。第 $n-1$ 笔是卖单,第 $n$ 笔是买单,成交量1000股。
- $d_n=1, q_n=1000$。$d_{n-1}=-1, q_{n-1}$假设为-500。
- $d_n - d_{n-1} = 1 - (-1) = 2$。
- 价格变化 $\Delta p \approx \lambda_0 d_n + \lambda_1 q_n + \gamma_0(d_n-d_{n-1}) = 0.005 \times 1 + 10^{-6} \times 1000 + 0.003 \times 2 = 0.005 + 0.001 + 0.006 = 0.012$。价格预计上涨$0.012。
- 对比: 场景2比场景1多出来的$0.006,就是由于价格从卖盘价跳到买盘价造成的“反弹”,它反映了订单处理成本。而两场景中共同的$0.006部分,则反映了这笔1000股买单所带来的信息冲击。
本段详细介绍了用于估计价格冲击的Glosten-Harris(1988)模型。该模型通过对逐笔交易数据进行回归,能够将价格变化分解为反映信息含量的“逆向选择成本”(由$\lambda_0, \lambda_1$度量)和反映交易执行成本的“订单处理成本”(由$\gamma_0, \gamma_1$度量)。这是后续分析的核心工具。
本段的目的是为价格冲击的测量提供一个坚实的、被学术界广泛认可的理论和方法论基础。通过引入并解释这个经典模型,作者使其后续的分析变得科学、严谨和可信,而不是凭感觉或使用随意定义的方法。
📜 [原文34]
[^13]为了比较整数时间点交易和非整数时间点交易之间的价格冲击,我们引入了一个虚拟变量 $\mathbf{1}_{\text { 5min, } n}$,它指示第 $n$ 次交易是否属于 5 分钟整数时间点(如上午 9:35:00、9:40:00 等)的 3 秒间隔内,第 4 节记录了这些时间点存在强烈的成交量激增。因此,我们调整后的价格冲击回归为:
对于美国和中国股票市场数据集中的每只股票,我们估计一个价格冲击回归 (15) [^23]。图 9 总结了美国和中国市场的回归结果。由于 (15) 的估计参数取决于股票价格的大小,我们在这些图中通过股票价格对所有参数估计值进行了标准化。
本段在经典GH模型的基础上,引入了创新的修改,以直接检验本文的核心假设。
- 研究目的: “比较整数时间点交易和非整数时间点交易之间的价格冲击”。
- 整数时间点: 指的是那些我们已经发现存在成交量激增的时刻,这里以5分钟的整数倍为例(9:35:00, 9:40:00, ...)。
- 非整数时间点: 其他所有时间。
- 引入虚拟变量 (Dummy Variable):
- $\mathbf{1}_{\text{5min}, n}$: 这是一个指示变量,用于标记交易发生的时间。
- 定义: 如果第 $n$ 笔交易发生的时间,在某个5分钟整数倍时刻的“3秒间隔内”(例如,9:35:00.000 到 9:35:02.999),那么 $\mathbf{1}_{\text{5min}, n} = 1$。否则,$\mathbf{1}_{\text{5min}, n} = 0$。
- 选择3秒间隔的理由: 因为成交量激增不是一个无限窄的脉冲,而是在整数时间点周围一个非常短暂的时间窗口内的集中爆发。3秒是一个合理的窗口选择。
- 调整后的回归模型 (公式 15):
- 核心思想: 将虚拟变量 $\mathbf{1}_{\text{5min}, n}$ 与原始GH模型中的每一项进行“交互”。
- 解读交互项:
- $\lambda_0 d_n + \tilde{\lambda}_0 d_n \mathbf{1}_{\text{5min}, n}$:
- 当交易不在5分钟整数点时($\mathbf{1}=0$),交易方向的冲击是 $\lambda_0$。
- 当交易在5分钟整数点时($\mathbf{1}=1$),交易方向的冲击是 $\lambda_0 + \tilde{\lambda}_0$。
- 因此,$\tilde{\lambda}_0$ 衡量的是,在整数时间点,交易方向的价格冲击额外增加了多少。
- 同理,$\tilde{\lambda}_1, \tilde{\gamma}_0, \tilde{\gamma}_1$ 分别衡量了在整数时间点,交易数量冲击、固定订单处理成本、可变订单处理成本的额外增量。
- 核心假设检验:
- 我们关心的是这四个带波浪线(tilde)的系数:$\tilde{\lambda}_0, \tilde{\lambda}_1, \tilde{\gamma}_0, \tilde{\gamma}_1$。
- 如果我们的假设(整数时间点的交易包含更多信息)成立,那么我们预期在这些时间点的逆向选择成本(信息冲击)会更高。
- 待检验的假设: $\tilde{\lambda}_0 > 0$ 且 $\tilde{\lambda}_1 > 0$。
- 同时,由于信息不对称更严重,做市商的风险也更大,他们可能会要求更高的订单处理成本作为补偿,因此也可能预期 $\tilde{\gamma}_0 > 0$ 且 $\tilde{\gamma}_1 > 0$。
- 模型估计和结果展示:
- 对数据集里的每只股票,都单独运行一次公式(15)的回归。
- 图9用来总结所有股票的回归结果(很可能是展示这些系数估计值的分布,如箱线图或直方图)。
- 标准化处理: 由于像 $\lambda_1$ 这样的系数,其单位是“美元/股”,会受到股价本身大小的影响(1000美元的股票和10美元的股票,其$\lambda_1$会差很多)。为了跨股票比较,作者将所有估计出的参数都除以该股票的平均价格,进行标准化。
- 公式 (15):
- $\mathbf{1}_{\text{5min}, n}$: 虚拟变量,若第n笔交易在5分钟整数点附近则为1,否则为0。
- $\lambda_0, \lambda_1, \gamma_0, \gamma_1$: 基准的价格冲击参数(非整数时间点)。
- $\tilde{\lambda}_0, \tilde{\lambda}_1, \tilde{\gamma}_0, \tilde{\gamma}_1$: 价格冲击在整数时间点的额外增量。这是我们关注的焦点。
- 继续用之前的例子,假设回归得到: $\lambda_0 = 0.005$, $\tilde{\lambda}_0 = 0.004$。
- 场景1: 非整数点的买单: $\mathbf{1}=0$。
- 方向冲击 = $\lambda_0 = 0.005$。
- 场景2: 整数点的买单: $\mathbf{1}=1$。
- 方向冲击 = $\lambda_0 + \tilde{\lambda}_0 = 0.005 + 0.004 = 0.009$。
- 结论: 整数时间点的买单,其所包含的信息冲击(0.009)几乎是非整数时间点(0.005)的两倍。这表明整数时间点的交易确实传递了更多信息。
本段通过在经典的Glosten-Harris模型中巧妙地引入一个时间虚拟变量及其与所有项的交互项,构建了一个可以直接比较整数时间点与非整数时间点价格冲击差异的扩展模型(公式 15)。模型的核心是检验代表价格冲击“额外增量”的系数($\tilde{\lambda}_0, \tilde{\lambda}_1$ 等)是否显著为正。
本段的目的是设计一个能够精准回答本节研究问题的计量工具。它展示了作者如何将一个标准模型进行创新性改造,以服务于自己独特的研究目的。这是从“使用现有工具”到“改造和发明新工具”的提升,体现了高水平的研究能力。
📜 [原文35]
绝大多数股票在价格冲击回归中产生正的参数估计值。特别是,美国市场中 $\tilde{\lambda}_{0}, \tilde{\lambda}_{1}, \tilde{\gamma}_{0}$ 和 $\tilde{\gamma}_{1}$ 估计值为正的股票比例分别为 99.2%、74.2%、99.6% 和 81.5%。中国市场的结果也类似。
$\tilde{\lambda}_{0}$ 和 $\tilde{\lambda}_{1}$ 的正值意味着平均而言,整数时间点的单位交易价格冲击高于非整数时间点。类似地,$\tilde{\gamma}_{0}$ 和 $\tilde{\gamma}_{1}$ 的正值意味着整数时间点的价差和交易成本高于非整数时间点。这两者都表明这些成交量激增与更高的信息含量相关 [^24]。
本段开始解读图9所示的回归结果,并阐述其经济学含义。
- 总体结果: “绝大多数股票在价格冲击回归中产生正的参数估计值。”
- 这指的是所有八个参数($\lambda_0, \tilde{\lambda}_0, \dots$)。它们理论上都应该为正,这个结果符合预期,说明模型是合理的。
- 核心结果:美国市场:
- 作者重点报告了四个带波浪线(tilde)的增量参数为正的股票占比。
- $\tilde{\lambda}_0$ (方向冲击增量): 99.2% 的股票为正。这是一个压倒性的结果,说明对于几乎所有股票,整数时间点交易的方向本身就比平时包含了更多的信息。
- $\tilde{\gamma}_0$ (固定成本增量): 99.6% 的股票为正。同样是压倒性的结果,说明在整数时间点,做市商收取的固定价差显著更高。
- $\tilde{\lambda}_1$ (数量冲击增量): 74.2% 的股票为正。结果为正的占多数,但不如方向冲击那么普遍。这可能意味着在整数时间点,交易的“动作”比交易的“大小”更重要。
- $\tilde{\gamma}_1$ (可变成本增量): 81.5% 的股票为正。多数为正。
- 核心结果:中国市场: “中国市场的结果也类似。” 作者在这里做了简化处理,没有列出具体数字,但暗示了结论的普适性。
- 解读结果的经济学含义:
- 解读 $\tilde{\lambda}$: “$\tilde{\lambda}_{0}$ 和 $\tilde{\lambda}_{1}$ 的正值意味着平均而言,整数时间点的单位交易价格冲击高于非整数时间点。”
- 这是对结果最直接的翻译。在这些成交量激增的时刻,交易对价格的永久性影响更大。
- 解读 $\tilde{\gamma}$: “$\tilde{\gamma}_{0}$ 和 $\tilde{\gamma}_{1}$ 的正值意味着整数时间点的价差和交易成本高于非整数时间点。”
- 做市商在这些时刻会把买卖价差拉得更开,要求更高的补偿。
- 综合解读: “这两者都表明这些成交量激增与更高的信息含量相关 [^24]”。
- 这是最终的经济学结论。为何价格冲击更高?因为交易中包含的信息更多。为何交易成本更高?因为市场上的信息不对称程度在这些时刻加剧了,做市商为了保护自己不被知情交易者“收割”,必须拉大价差,这本身就是信息不对称加剧的信号。
- [^24]: 脚注可能指向了将“价差扩大”也解释为信息不对称信号的文献。
- 比例不等于显著性: 这里报告的是系数为正的股票“比例”,这与系数是否“统计显著”为正是两个概念。一个系数可能为正但统计上不显著。图9本身会提供更完整的关于显著性的信息(例如,通过展示系数的t值分布)。但如此高的正值比例,本身已经是一个非常强的证据。
- 经济显著性: 除了符号和统计显著性,冲击增量的大小(经济显著性)也很重要。图9的分布图可以告诉我们这些增量普遍有多大。
本段通过报告修改后的Glosten-Harris模型回归结果,发现对于绝大多数股票,在成交量激增的整数时间点,代表信息含量的价格冲击参数($\tilde{\lambda}_0, \tilde{\lambda}_1$)和代表交易成本的价差参数($\tilde{\gamma}_0, \tilde{\gamma}_1$)都显著增加。这一发现有力地证明了,这些周期性的成交量激增并非随机交易的堆积,而是由信息含量更高的交易构成的。
本段的目的是呈现第五项证据的核心数据结果,并给出直接的经济学解释。通过量化地展示tilde系数的压倒性正值比例,作者将“整数时间点交易更具信息性”这一假设从猜想变为了有数据支持的结论,从而为“算法交易驱动论”提供了来自信息层面的强力佐证。
📜 [原文36]
这些交易很可能是由交易算法触发的,这些算法利用基于在整数时间点更新的输入数据和信号的高频信息,或者是来自代表机构投资者的经纪商交易算法的持续交易,这也可能被 Sağlam (2020) 记录的订单预测策略放大。
[^14]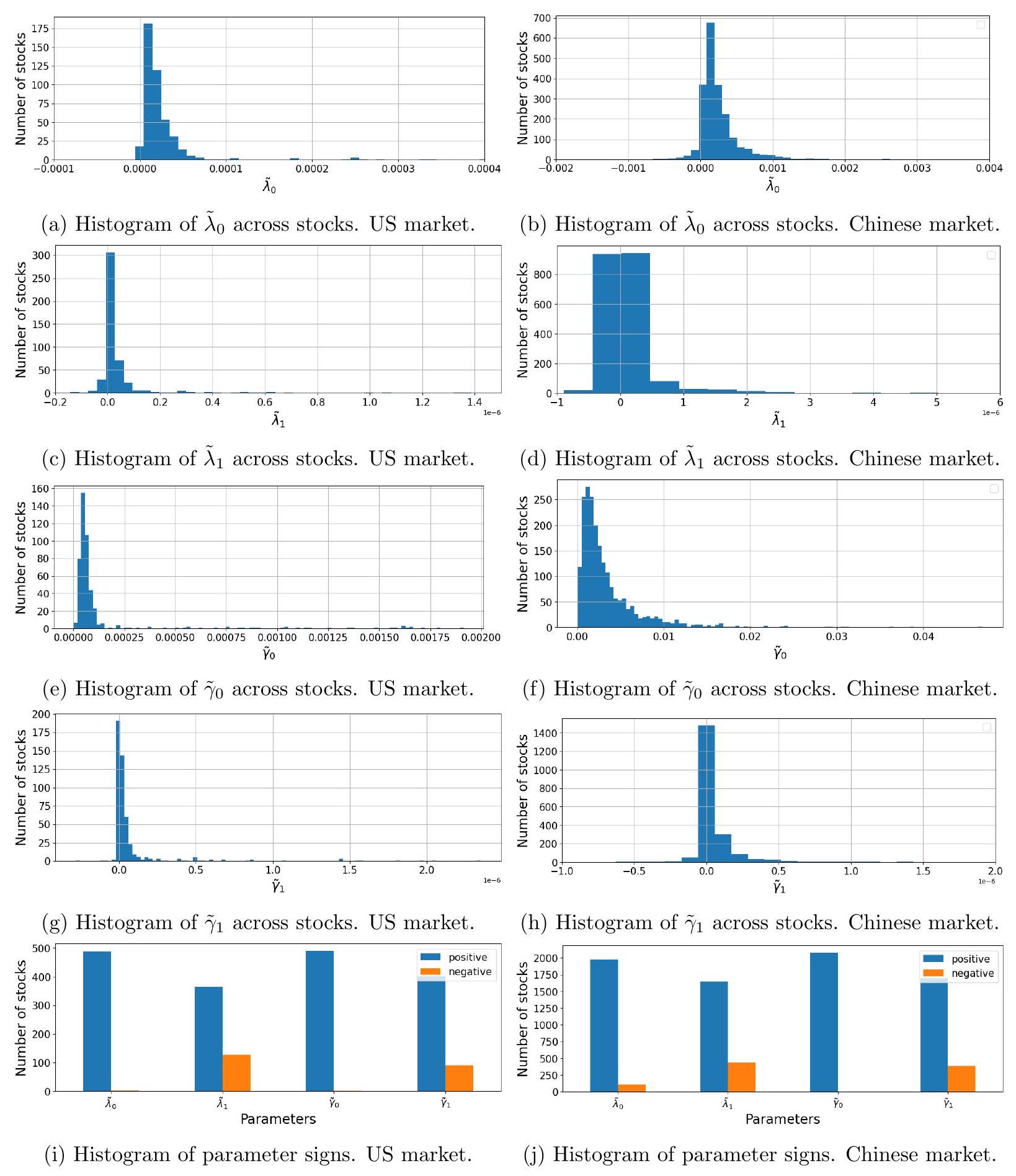
图 9:美国市场股票(左侧五张图)和中国市场股票(右侧五张图)的价格冲击回归总结。在 (a)-(h) 中,参数值已按股票价格标准化。
本段在上一段结论的基础上,进一步推测了产生这种“高信息量周期性交易”的具体机制。
- 核心归因: “这些交易很可能是由交易算法触发的”。这是本节最终的落脚点。
- 两种可能的算法机制:
- 机制一:基于定时更新信号的策略:
- “这些算法利用基于在整数时间点更新的输入数据和信号的高频信息”。
- 解释: 许多交易算法的输入数据本身就是以固定的时间间隔生成的。例如:
- 数据供应商: 可能会在每分钟、每5分钟的整数点,打包发布新的数据产品(如另类数据、因子得分等)。
- 策略本身: 算法可能会自己构建“时间棒”(time bars),例如每10秒计算一次收益率、波动率等技术指标。
- 执行逻辑: 一旦新的数据或信号在整数时间点生成,算法会立刻进行计算和决策,并触发交易。因为这些新信号是高频信息,所以基于它们产生的交易自然就包含了更高的信息含量和价格冲击。
- 机制二:经纪商执行算法的持续交易:
- “或者是来自代表机构投资者的经纪商交易算法的持续交易”。
- 解释: 这里指的是像前面提过的VWAP、TWAP这类执行算法。它们被设定为在一天内持续不断地拆分和执行大订单。这些算法的行为模式本身可能就具有周期性(例如,TWAP算法每隔固定时间就抛出一笔小单)。
- 虽然单笔执行订单的信息含量可能不高,但当大量机构的执行算法都在同一时间点(如整数分钟)巧合地执行时,它们的汇集效应也可能被市场解读为一种“信息”,从而产生价格冲击。
- 放大机制:订单预测策略:
- “这也可能被 Sağlam (2020) 记录的订单预测策略放大。”
- 解释: 市场上存在一类“掠食性”的高频交易策略,它们的任务就是预测其他大型交易者(特别是执行算法)的行为模式。
- 放大过程:
- 掠食性算法发现,很多VWAP算法都喜欢在整数分钟点执行交易。
- 于是,在整数分钟点到来之前的一瞬间,掠食性算法会抢先进行交易(例如,如果预测到将有大买单,就提前买入,推高价格),然后再把股票卖给那些“迟到”的VWAP算法,从中牟利。
- 这种抢跑和预测行为,会加剧整数时间点的交易拥挤和价格冲击,从而“放大”了我们观察到的现象。
图9解读
- 图表结构: 图9由10个子图构成,左5个是美国市场,右5个是中国市场。其中,(a)-(h) 这8个图,分别对应8个参数 ($\lambda_0, \tilde{\lambda}_0, \lambda_1, \tilde{\lambda}_1, \gamma_0, \tilde{\gamma}_0, \gamma_1, \tilde{\gamma}_1$) 的估计值分布(很可能是直方图或核密度估计图)。
- 核心观察点: 我们应该重点关注带波浪线的参数图,即 (b) $\tilde{\lambda}_0$, (d) $\tilde{\lambda}_1$, (f) $\tilde{\gamma}_0$, (h) $\tilde{\gamma}_1$。
- 预期景象: 根据上一段的文字描述,这些图的绝大部分质量(面积)都应该分布在x轴的正半轴,即绝大多数股票的这些参数估计值都大于0。特别是图(b) $\tilde{\lambda}_0$ 和 (f) $\tilde{\gamma}_0$,其分布应该几乎完全在正半轴。这为“99.2%和99.6%为正”提供了视觉证据。
- 标准化: 图注提到参数已按股价标准化,这使得跨股票的分布图可以直接比较。
本段为“整数时间点的交易富含信息”这一发现,提供了三个具体的微观机制解释:1) 算法对定时更新的高频信息做出反应;2) 大量经纪商执行算法在整数时间点的同步交易;3) 掠食性算法对这些同步交易的预测和抢跑,进一步放大了效应。这些机制共同描绘了一幅由不同类型的交易算法相互作用、共同催生出周期性高信息含量交易的生动图景。
在给出了“是什么”(整数点交易有高价格冲击)的结论后,本段试图回答“为什么”和“如何发生”。通过提供具体的、符合市场实践的微观机制,作者使得其统计发现不再是空中楼阁,而是有了坚实的现实基础。这大大增强了论证的深度和完整性。
5.3 替代渠道
53.1 散户交易控制
📜 [原文37]
在本节中,我们展示了在控制了几个散户交易代理指标后,我们记录的周期性交易行为仍然是稳健的,控制手段包括剔除散户交易数据、剔除碎股交易、比较 Robinhood 宕机日与正常日,以及 2020 年新冠疫情爆发期间的时间序列模式。
这是第六项证据的开篇,这项证据采用的是“排除法”的逻辑。
- 提出一个替代性假说: 周期性是否可能不是由机构性的算法交易驱动,而是由大量的散户交易(Retail Trading)驱动的?
- 理由: 散户投资者也可能表现出某种“同步”行为。例如,他们可能都喜欢在整数时间点查看行情并做出交易决策;或者,他们可能受到社交媒体上某些“大V”在特定时间喊单的影响。
- 如果这个替代假说成立,那么本文的核心论点就会受到挑战。因此,必须对这个可能性进行检验和排除。
- 本节目标: “我们展示了在控制了几个散户交易代理指标后,我们记录的周期性交易行为仍然是稳健的”。
- 核心思想: 如果周期性是由散户交易驱动的,那么当我们把散户交易从数据中“拿走”之后,周期性应该会显著减弱或消失。
- 预期结果: 作者预告,实验结果将表明,即使在各种“控制”了散户交易影响的场景下,周期性依然强劲。这就意味着,散户交易不是周期性的主要驱动力。
- 介绍四种控制/检验方法: 作者设计了四种不同的、巧妙的方法来检验散户交易的潜在影响。
- 方法一:直接剔除识别出的散户交易: 使用一个成熟的算法(BJZZ算法)来识别并剔除数据中的散户交易,然后对剩下的“非散户交易”数据重新进行谱分析。
- 方法二:剔除碎股/小额交易: 碎股和小额交易被认为是散户和算法的混合体。剔除它们是一种更粗略但有用的控制。如果剔除后周期性仍在,说明至少不是由这部分交易驱动的。
- 方法三:利用Robinhood宕机日进行自然实验: Robinhood是美国散户最主要的交易平台之一。当它宕机时,大量的散户无法交易。通过比较宕机日和正常日的周期性强度,可以判断散户的缺席是否对周期性有影响。
- 方法四:利用2020年新冠疫情进行时间序列分析: 2020年疫情爆发初期,是历史上散户入市最疯狂的时期之一。通过观察这一时期周期性强度的变化,可以反推散户的大量涌入是增强了还是减弱了周期性。
本段阐述了第六项证据的研究设计,其目的是检验并排除“散户交易驱动论”这一重要的替代假说。作者提出了四种精巧的检验方法:直接剔除、部分剔除、利用平台宕机的自然实验、以及利用疫情期间散户潮的时间序列分析。通过这些多角度的控制实验,作者旨在证明周期性交易行为的稳健性,并将其来源更明确地指向非散户的专业交易者。
在科学论证中,仅仅提供支持自己假说的证据是不够的,还必须有力地回应和排除其他可能的解释。本节的存在,就是为了处理一个最显而易见的“竞争性假说”。通过系统性地证伪“散户交易驱动论”,作者可以大大巩固其“算法交易驱动论”的可信度,使论证更加无懈可击。
📜 [原文38]
首先,在排除了由 Boehmer et al. (2021) 的 BJZZ 算法识别的美国市场散户交易后,成交量中的周期性强度仍然稳健。图 10a 显示了排除散户交易后美国市场不同股票的 fVRs 箱线图。结果与图 4 几乎相同,证明成交量中的周期性不可能由散户交易驱动,至少不能由 BJZZ 算法识别出的那些交易所驱动。
这是对第一个控制实验的详细描述和结果解读。
- 实验方法:
- 核心工具: BJZZ 算法。这是由 Boehmer, Jones, Zryumov, and Zhang (2021) 开发的一种 widely-used 的算法,用于从逐笔交易数据中识别哪些交易可能是由散户发起的。该算法的准确性在学术界得到了较好的认可。
- 操作步骤:
- 获取原始的逐笔交易数据。
- 应用 BJZZ 算法,给每一笔交易打上“散户”或“非散户”的标签。
- 构建一个新的成交笔数时间序列,该序列只包含被标记为“非散户”的交易。
- 对这个“净化”过的时间序列,重新进行与第4节完全相同的谱分析,计算 fVR。
- 结果展示:
- 图 10a 展示了新计算出的 fVR 的箱线图。
- 核心观察: “结果与图 4 几乎相同”。图4是基于全部交易数据计算出的原始fVR箱线图。两张图“几乎相同”意味着:
- 在各个频率上,fVR的中位数、四分位距等分布特征都没有发生显著变化。
- 在关键频率(10秒、1分钟等)上的周期性强度,在剔除了散户交易后,几乎没有减弱。
- 结论与推断:
- 直接结论: “证明成交量中的周期性不可能由散户交易驱动”。
- 逻辑: 如果散户交易是周期性的主要来源,那么拿掉它们之后,周期性应该会大幅下降。但事实是周期性几乎没变。这说明,驱动周期性的交易,主要就存在于我们剩下的那部分“非散户交易”中。
- 严谨的限定: “至少不能由 BJZZ 算法识别出的那些交易所驱动”。作者再次展现了学术严谨性。他们承认,结论的有效性受限于 BJZZ 算法的准确性。如果存在大量 BJZZ 算法没能识别出来的“隐形”散户,且这些散户恰好是周期性的来源,那么结论就可能不成立。但鉴于 BJZZ 算法是当前领域的SOTA(state-of-the-art),这个限定更多是一种形式上的严谨,结论本身是相当可信的。
第一个控制实验通过使用BJZZ算法剔除已识别的散户交易,并发现周期性强度几乎不受影响。这一结果(如图10a所示)有力地证明了,周期性并非源于散户交易,而是源于非散户的机构性或专业性交易。
📜 [原文39]
其次,在排除了美国市场中严格少于 100 股的碎股交易后,成交量中的周期性强度仍然稳健 [^25]。正如 O'Hara, Yao, and Ye (2014) 所指出的,相当比例的碎股交易也可能来自散户投资者。图 10b 显示了排除碎股交易后美国市场的 fVRs 箱线图。结果再次与图 4 几乎相同。
这是第二个控制实验。
- 实验方法:
- 剔除对象: “严格少于 100 股的碎股交易 (odd-lot trades)”。在美国市场,100股被称为一个“整手”(round lot),小于100股的交易被称为碎股。
- 操作步骤:
- 筛选原始交易数据,将所有交易量小于
100 股的交易筛选出来,然后丢弃它们。
- 构建一个新的成交笔数时间序列,该序列只包含交易量大于或等于 100 股的“整手交易”。
- 对这个新的时间序列重新进行谱分析,计算 fVR。
- 实验的基本逻辑:
- O'Hara, Yao, and Ye (2014) 这篇重要文献指出,碎股交易的来源是复杂的,既有可能是算法交易(订单拆分的结果),也“可能来自散户投资者”。
- 因此,剔除碎股可以看作是对散户交易影响的一种(不完美的)控制。如果周期性的来源主要是散户的小额碎股交易,那么剔除它们后周期性应该会减弱。
- 结果展示与解读:
- 图 10b 展示了剔除碎股后的 fVR 箱线图。
- “结果再次与图 4 几乎相同”。这与第一个实验的结论如出一辙。剔除掉所有小于100股的交易后,周期性的强度和模式几乎没有任何变化。
- 结论: 周期性的来源不是碎股交易。结合前文,周期性源于成交笔数,但并非源于那些小额的碎股成交笔数,而是源于那些“整手”的成交笔数,这更符合机构和专业算法交易的行为特征。
- [^25]: 这个脚注可能指向美国市场关于碎股定义的具体规则或数据来源。
- 碎股来源的复杂性: 正如 O'Hara 等人指出的,碎股并非散户专属。算法交易本身就会产生大量碎股。因此,这个实验的结论应该谨慎地解读为“周期性并非由那些可能包含大量散户的碎股部分所驱动”,而不是说算法交易产生的碎股与周期性无关。但无论如何,它都削弱了“散户驱动论”。
第二个控制实验通过剔除小于100股的碎股交易,发现周期性强度依然稳健。这个结果进一步排除了周期性来源于小额散户交易的可能性,并将来源更精确地指向了整手交易,这更符合专业算法交易的特征。
📜 [原文40]
第三,在使用 Jiang et al. (2022) 的代理指标排除中国市场中严格少于 10,000 元人民币的小额交易后,成交量中的周期性强度仍然稳健 [^26]。图 10c 显示了排除小额交易后中国市场的 fVRs 箱线图。结果再次与图 4 几乎相同。
这是第三个控制实验,是中国市场版本的“剔除小额交易”。
- 实验方法:
- 剔除对象: “严格少于 10,000 元人民币的小额交易”。在中国市场,由于股价差异大,使用固定的“股数”作为小额交易的标准可能不合适。因此,研究者通常使用“交易金额”作为划分标准。
- 代理指标来源: 这个 10,000 元的阈值不是随意设定的,而是来源于 Jiang et al. (2022) 的研究,他们发现这个金额可以作为识别中国市场散户交易的一个有效代理指标。
- 操作步骤:
- 筛选中国市场的交易数据,将所有交易额小于 10,000 元的交易剔除。
- 用剩下的“大额”交易构建新的成交笔数时间序列。
- 对这个新序列进行谱分析,计算 fVR。
- 结果展示与解读:
- 图 10c 展示了剔除小额交易后中国市场的 fVR 箱线图。
- “结果再次与图 4 几乎相同”。这里的图4应指图4中关于中国市场的部分。结论与美国市场的实验完全一致:剔除掉被认为是散户主力的小额交易后,周期性强度几乎没有变化。
- 结论: 中国市场的周期性也不是由小额散户交易驱动的。这一发现在跨市场的检验中保持了一致性。
- [^26]: 该脚注指向 Jiang et al. (2022) 的文献,为10,000元这个阈值的选择提供了依据。
- 阈值的敏感性: 结论是否对 10,000 元这个具体阈值敏感?严谨的分析可能会测试不同的阈值(如5,000元,20,000元),看结论是否依然成立。本文可能在附录或未报告的分析中做过此类稳健性检验。
第三个控制实验将分析扩展到中国市场,通过剔除被认为是散户行为代表的小额交易(<10,000元),再次发现周期性强度保持稳健。这表明,无论在美国还是中国市场,周期性的来源都不是小额的散户交易。
📜 [原文41]
第四,在 Robinhood 宕机日及其前后,成交量中的周期性强度仍然稳健。特别是,我们从其官方网站上识别了 2019-2021 年期间 Robinhood 的 43 次平台宕机 [^27],并计算了宕机日以及紧接这些日期前一周和后一周的周期性强度,总结在图 11 中。在能够交易的散户投资者较少的宕机日,周期性强度与周围其他日子相似,甚至略高。
这是第四个控制实验,采用的是一种巧妙的“自然实验”方法。
- 实验设计:利用平台宕机作为自然实验:
- Robinhood: 是美国一家拥有海量年轻用户的互联网券商,被视为散户交易的代名词。
- 自然实验 (Natural Experiment): 指的是现实世界中发生的、如同“随机分配”了实验组和对照组的事件。Robinhood 的平台宕机,就相当于一个“实验”,它将市场上的交易者“随机地”分成了两组:
- 处理组 (Treatment Group): 依赖 Robinhood 平台的散户,他们在宕机日无法交易(受到了“处理”)。
- 控制组 (Control Group): 其他所有交易者(机构、算法交易员、使用其他券商的散户),他们可以正常交易。
- 逻辑: 如果周期性是由 Robinhood 上的散户驱动的,那么在他们无法交易的宕机日,周期性强度应该会显著下降。
- 数据与方法:
- 事件识别: 作者找到了 43 个 Robinhood 平台宕机的日子。[^27] 指向了数据来源,即其官方网站,保证了事件的真实性。
- 分析窗口: 不仅仅看宕机日当天,还看了“前一周和后一周”,这是一种标准的事件研究方法,用于建立一个“正常水平”的基准,并观察事件冲击的持续性。
- 度量指标: 计算每天的周期性综合强度 peri 值。
- 结果解读:
- 结果总结在图11中。
- “在...宕机日,周期性强度与周围其他日子相似,甚至略高。”
- 相似: 意味着散户的缺席对周期性没有负面影响。
- 甚至略高: 这是一个更强的结论。它暗示,散户的交易活动可能平时是作为“噪声”存在的,他们的缺席反而让由专业交易者主导的周期性信号变得更“纯净”、更强了。
第四个控制实验利用 Robinhood 平台宕机作为自然实验,发现当大量散户无法交易时,市场的周期性强度并未减弱,甚至略有增强。这提供了非常有力的证据,表明散户交易不是周期性的驱动力,反而可能起到了干扰作用。
📜 [原文42]
最后,我们记录了 2020 年 4 月至 6 月美国市场周期性强度的下降。
[^15]
图 10:排除某些类型交易时不同度量指标的频率方差比 (fVR) 箱线图。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为我们在模型中包含了 $n=500$ 个周期分量。
图 11:发生宕机的日期以及这些日期之前和之后一周内的 peri 值柱状图。例如,柱子 0(红色柱子)是所有宕机日期平均日内交易量的 peri 值,柱子 1 是所有宕机日期后一天平均日内交易量的 peri 值。
在新冠疫情爆发初期,随着大量散户投资者涌入市场 (Eaton et al., 2022),市场的月度 peri 减少了一半以上,从平均约 0.12-0.16 降至 0.06 左右,如图 12 所示。这提供了另一个支持性证据,即散户交易可能不是周期性背后的驱动力。
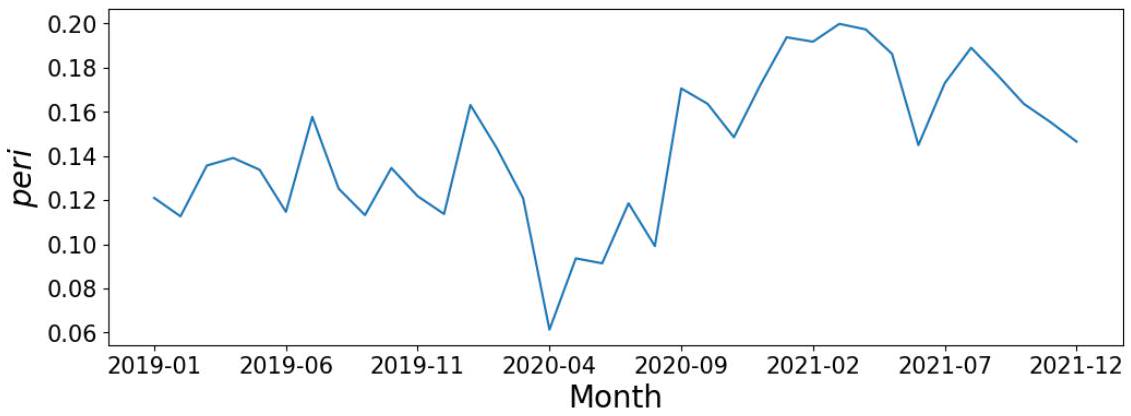
图 12:2019-2021 年美国市场每月估计的 peri 值。
这是第五个,也是最后一个检验散户交易影响的实验。它同样利用了一个宏观的自然实验。
- 实验设计:利用新冠疫情初期的散户潮:
- 背景: 2020年初新冠疫情爆发,美国实行封锁政策,许多人居家隔离。同时,政府发放了经济刺激支票。这两个因素导致了史无前例的散户交易热潮,大量新手投资者涌入股市。这一现象已被 Eaton et al. (2022) 等多篇学术文献记录和证实。
- 时间窗口: 2020年4月至6月,是这波散户潮最汹涌的时期。
- 逻辑: 这个时期为我们提供了一个“散户交易占比极高”的独特样本。如果散户交易是周期性的驱动力,我们应该看到 peri 在这段时间里飙升。反之,如果散户交易是噪声,它应该会“稀释”由专业交易者产生的周期性信号,导致 peri 下降。
- 结果解读:
- 结果展示在图12,一个按月计算的peri值时间序列图。
- 核心观察: “市场的月度 peri 减少了一半以上,从平均约 0.12-0.16 降至 0.06 左右”。图12会清晰地显示,在2020年中间那几个月,peri值出现了一个显著的“凹陷”。
- 结论: “这提供了另一个支持性证据,即散户交易可能不是周期性背后的驱动力。”
- 这个结果与Robinhood宕机日的发现完美呼应。散户的大量涌入,不仅没有增强周期性,反而使其显著减弱。
- 这强烈地表明,散户交易的行为模式是相对随机、无规律的,当它们在市场总交易量中的占比提高时,就会像往一杯纯净水里倒入大量泥沙一样,使得水(市场交易量)的“清澈度”(周期性信号)大幅下降。
图10、11、12的综合解读
- 图10 (a, b, c): 这组图是“剔除法”的证据。它们显示,无论是剔除BJZZ算法识别的散户,还是剔除碎股和小额交易,剩下的交易数据依然表现出和原来一样强的周期性。结论:周期性存在于非散户、非碎股的大额交易中。
- 图11: 这是“缺席法”的证据。它显示,当一大群散户(Robinhood用户)集体缺席时,周期性并未减弱。结论:驱动周期性的不需要这些散户。
- 图12: 这是“稀释法”的证据。它显示,当市场上充斥着大量散户时,周期性反而被稀释和削弱了。结论:散户交易是周期性的“敌人”而不是“朋友”。
第五个控制实验利用2020年疫情期间散户大量涌入市场的事件,发现市场的周期性强度在此期间不升反降,减少了一半以上。这与Robinhood宕机日的结论一致,共同构成了强有力的证据,表明散户交易不仅不是周期性的来源,反而是一种破坏和削弱周期性信号的“噪声”。至此,通过五种不同的方法,作者系统性地排除了“散户交易驱动论”。
53.2 新闻文章是周期性发布的吗?
📜 [原文43]
到目前为止,我们已经表明周期性强度与算法交易的代理指标正相关,成交量激增产生更高的价格冲击,且不太可能仅由散户交易驱动。在本节中,我们探讨周期性交易行为是否可能由周期性新闻文章的消费驱动。
这是第七项,也是最后一项证据的开篇。它转向探讨另一个重要的替代假说。
- 承上启下: 作者首先简要回顾了前面六项证据的结论:
- 证据1-3: 周期性的特征(源于笔数、与代理指标正相关、历史演进吻合)与算法交易一致。
- 证据4-5: 成交量激增时段的交易具有高信息含量,符合知情的算法交易特征。
- 证据6: 周期性不可能是由散户交易驱动。
- 提出新的替代假说: “探讨周期性交易行为是否可能由周期性新闻文章的消费驱动。”
- 假说内容: 也许算法交易只是一个“中间人”。真正的源头是新闻的发布。如果新闻机构(如路透、彭博)有在整数分钟/秒发布新闻的习惯,那么交易算法可能只是在“同步地”读取和反应这些周期性发布的新闻,从而导致了周期性的交易。
- 这个假说的重要性: 如果这个假说成立,那么周期性的根源就是“信息发布的周期性”,而不是算法交易内在的、自主的定时行为。这将大大改变我们对这一现象的理解。
本段作为新一节的引言,在总结前文结论的基础上,提出了最后一个需要检验的替代假说:交易量的周期性是否根源于新闻发布的周期性。
📜 [原文44]
我们从 Ravenpack 获取已发布新闻文章的数据,这是一个被 70% 的最大对冲基金和资产管理公司采用的流行实时新闻数据库 [^28]。它包含来自
[^16]40,000 多个全球来源的新闻文章,包括优质新闻提供商、监管和新闻通讯社。它提供了每篇文章的毫秒级时间戳,并确定文章中提到了哪些公司。该数据集已在文献中广泛用于研究发布的新闻对金融市场的影响 (von Beschwitz, Keim, and Massa, 2020, Ben-Rephael et al., 2022; Chen and Li, 2023)。
本段详细介绍了用于检验“新闻周期性”假说的数据来源。
- 数据来源:Ravenpack:
- 这是一个商业化的、专业的金融新闻数据提供商。
- 权威性: 作者强调了它的行业地位——“被 70% 的最大对冲基金和资产管理公司采用”。这说明 Ravenpack 的数据是金融行业专业人士真正在使用的,用它来做研究非常贴近市场现实。[^28] 指向了这个说法的来源。
- 覆盖范围广: “40,000 多个全球来源”,包括了各种主流和专业的财经媒体、通讯社。这保证了数据的全面性。
- 数据特征:
- 毫秒级时间戳: 提供了新闻发布的精确时间,这对于研究高频周期性至关重要。
- 实体识别: 数据已经过处理,“确定文章中提到了哪些公司”。这使得研究者可以轻松地将新闻与特定的股票联系起来。
- 学术认可度:
- 作者引用了三篇顶级的金融学文献,它们都使用了 Ravenpack 数据。
- 作用: 这再次证明了使用该数据集进行研究的合理性和科学性,表明其数据质量和方法论已得到学术界的认可。
本段通过详细介绍 Ravenpack 数据的权威性、全面性、精确性和学术认可度,为后续的新闻周期性分析提供了坚实的数据基础。这表明作者在数据选择上是严肃和专业的。
📜 [原文45]
我们从 Ravenpack 中提取提及我们数据集中公司的新闻文章,并分析它们的周期性。匹配过程的细节见附录 H。对于每只股票,我们形成一个已发布新闻文章数量的时间序列,并使用第 3 节的方法进行谱分解。图 13 总结了每年发布新闻文章的 fVRs 分布,其中我们特意将其 y 轴与图 7 中的 y 轴对齐,以便比较。与成交量中持续增加的周期性形成鲜明对比的是,已发布的新闻文章在我们的样本期内没有显示出周期性。
图 13:两个市场在不同年份发布的关于新闻文章的频率方差比 (fVR) 柱状图。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为我们在模型中包含了 $n=500$ 个周期分量。y 轴与图 7 中的对齐。
本段描述了新闻周期性的分析方法和核心结果。
- 分析方法:
- 数据匹配: 将 Ravenpack 的新闻数据与研究中使用的股票列表进行匹配。附录 H 提供了技术细节。
- 构建时间序列: 对于每一只股票,构建一个新的时间序列。这个序列不再是成交笔数,而是“已发布新闻文章数量”。例如,在秒级上,如果在 10:05:30 这一秒有一篇关于苹果公司的新闻发布,那么苹果公司在该秒的序列值就为1,否则为0。
- 进行谱分析: 对这个“新闻数量”时间序列,采用与第3节和第4节完全相同的谱分解方法,计算出各个频率上的 fVR。
- 结果展示与解读:
- 结果总结在图13中,该图的结构与图7(交易量周期性的年度演变)非常相似。
- 特殊处理: 作者“特意将其 y 轴与图 7 中的 y 轴对齐”。这是一个非常重要的细节。通过使用相同的Y轴刻度,读者可以非常直观地、公平地比较交易量周期性和新闻周期性的强度。
- 核心观察 (图13): 图13中的所有柱子,无论哪个国家、哪一年、哪个频率,都紧紧地贴在0.2%的红色基准线附近。
- 与图7的“鲜明对比”: 图7中,交易量的周期性(特别是后期)柱子非常高,达到了百分之几。而图13中的新闻周期性柱子几乎是“隐形”的。
- 结论: “已发布的新闻文章在我们的样本期内没有显示出周期性。”
第七项证据的分析表明,使用行业标准的新闻数据库 Ravenpack,在对其进行与交易量完全相同的谱分析后,没有发现任何显著的周期性。新闻发布的fVR值在所有年份和频率上都接近于零,与交易量中观察到的强大且不断增长的周期性形成鲜明对比。这有力地排除了“交易量周期性是由新闻发布的周期性直接驱动”的假说。
📜 [原文46]
这一结果表明,我们在交易量中记录的强烈且持久的周期性不太可能直接由已发布新闻文章中的信息驱动,至少在 Ravenpack 数据集捕捉到的范围内是这样。然而,我们也提醒不要过度概括我们的发现。
我们的分析显示已发布的新闻文章没有显示出周期性,但这并不排除以周期性方式对新闻文章信息进行后期处理和消费的可能性。例如,投资者可能拥有计算机程序,以定期的时间间隔批量阅读新闻文章,并根据这些批次的输出采取行动。要确定性地研究这种可能性,需要获取资产管理公司内部的私人信息和数据,这是我们无法接触到的,留待未来研究。
这段是对新闻周期性分析的结论进行审慎的讨论和引申。
- 直接结论: “周期性不太可能直接由已发布新闻文章中的信息驱动”。
- 关键词“直接”: 周期性交易不是对“新闻发布”这个动作的被动、即时反应。
- 限定范围: “至少在 Ravenpack 数据集捕捉到的范围内是这样”。再次体现了学术严谨性,承认结论受限于数据源的覆盖范围。虽然 Ravenpack 已经很全面,但理论上仍可能存在它没覆盖到的、且恰好是周期性发布的“信息源”。
- 提醒不要过度概括 (Caveat): 这是本段的精髓,展现了作者深刻的思考。
- 区分“信息发布”与“信息处理”:
- 我们证伪了:“信息发布”是周期性的。
- 但我们没有也无法证伪:“信息处理和消费”是周期性的。
- 举例说明: “投资者可能拥有计算机程序,以定期的时间间隔批量阅读新闻文章,并根据这些批次的输出采取行动。”
- 场景: 一个对冲基金的算法,可能被设定为“每隔10秒,去 Ravenpack 的数据流里捞取过去10秒发布的所有新闻,然后运行一个自然语言处理模型进行情感分析,最后根据分析结果决定是否交易”。
- 结果: 在这个场景下,新闻的“发布”是随机、非周期性的,但算法对新闻的“读取、处理、行动”这个流程,是严格以10秒为周期的。这同样会导致10秒的周期性交易。
- 结论: 这种情况下,周期性的根源就不是“外部信息源的周期性”,而是“算法交易系统内在的工作模式(周期性处理)”。这反而支持了本文的核心论点——周期性是算法交易的内生特征。
- 指出研究边界与未来方向:
- 要检验“信息处理周期性”这个假说,需要什么?“需要获取资产管理公司内部的私人信息和数据”。例如,需要看到基金公司的代码、服务器日志、策略说明书等。
- 研究局限: 这是学术研究者几乎不可能拿到的数据。
- 未来研究 (Future Research): 作者优雅地将这个无法解决的问题,转化为一个开放性的、留给未来研究的课题。这是学术论文写作的标准做法。
本段在总结“新闻发布本身无周期性”的结论后,进行了深入的思辨,明确区分了“信息发布”和“信息处理”两个概念。作者指出,虽然排除了前者作为周期性的直接驱动力,但无法排除算法交易以周期性的方式“处理”非周期性的信息。这一讨论不仅没有削弱,反而巧妙地加强了“周期性源于算法内生行为”的核心论点,并指出了未来研究的方向。
5.4 总结
📜 [原文47]
总体而言,第 5.1.1 节至 5.3.2 节的结果与以下解释是一致的:周期性交易活动反映了具有重复且定期交易指令的交易算法的行为。鉴于当今金融市场中各种形式的算法的普及,广泛的投资者都可以促成这一现象,包括采用反转策略等算法交易策略的老练对冲基金,以及使用 VWAP 等经纪商执行算法进行买卖的传统资产管理公司。
这是对整个第5节所有七项证据的最高级别总结。
- 重申核心结论: “周期性交易活动反映了具有重复且定期交易指令的交易算法的行为。”
- 在完成了所有详尽的分析和替代假说的排除后,作者回到最初的论点,并以更强的信心重申它。
- 经过七轮“交叉火力”的检验,这个解释是唯一一个能与所有观察到的证据都“一致”的解释。
- 拓展贡献者的范围: “广泛的投资者都可以促成这一现象”。
- 作者在这里明确指出,周期性并非某一种特定类型的算法交易的专利,而是多种算法共同作用的结果。
- 举例说明:
- “采用反转策略等算法交易策略的老练对冲基金”:这代表了主动寻求阿尔法收益的“alpha策略”或“自营交易”算法。
- “使用 VWAP 等经纪商执行算法进行买卖的传统资产管理公司”:这代表了被动执行大额订单的“执行算法”。
- 意义: 这表明周期性是现代金融市场的一个结构性、系统性的特征,因为它是由市场上两类最主要的专业参与者(对冲基金和传统资管)所使用的、不同目的的交易算法共同造成的。它不是一个小众现象。
本段作为第5节的总结,高度概括了所有证据共同指向的结论:交易量的周期性是各类交易算法重复、定时行为的宏观体现。作者进一步指出,无论是主动的套利算法还是被动的执行算法,都可能对这一现象有所贡献,凸显了其普遍性。
📜 [原文48]
我们提供三点评论来使这些周期性交易行为合理化。首先,尽管我们没有在作为信息源示例的已发布新闻文章中发现周期性,但在实践中,投资者仍可能定期接收和处理信息,例如包括固定窗口的价格成交量柱线 (bars)、社交媒体帖子和信用卡交易等定期数据馈送,以及任何其他以定期时间间隔到达或生成的信号 [^29]。此外,算法交易员通常开发具有固定期限(如 10 秒或 5 分钟)的收益预测(或 alphas),并根据这些固定期限的预测执行交易。这些实践中的启发式方法意味着算法倾向于在具有整数开始时间和固定时间增量的循环中发送重复的交易指令。毕竟,很难想象有人会使用 3.1415926 分钟的价格成交量柱线作为算法的输入,或预测 3.1415926 分钟后的收益。
[^17]其次,我们的发现与定期或集群交易量的均衡模型的含义一致。例如,投资者可能会在定期时间进行交易,作为一种阳光交易 (sunshine trading) 以降低交易成本 (Admati and Pfleiderer, 1991),并且可能会在一个交易所集群交易以获得更好的流动性 (Pagano, 1989)。我们的发现不仅意味着交易集中在几个交易场所中的一个,还意味着交易在时间维度上的集中。事实上,对于具有巨大市场影响的有信息的算法交易员来说,在流动性激增的定期成交量集群处进行交易可能有助于降低其交易成本。
最后,Bogousslavsky (2016) 表明,不频繁的再平衡可能导致收益率和成交量的自相关。也有充分的证据表明,来自某些机构投资者的基金流在日、月和季度频率上表现出强烈的自相关和周期性模式(例如,参见 Guercio and Tkac (2002), Frazzini and Lamont (2008), Campbell, Ramadorai, and Schwartz (2009), Lou (2012), and Kamstra et al. (2017))。我们的发现可以被视为这些行为的高频版本。
在得出结论后,本段从更深层次的理论和实践角度,提供了三个“合理化解释”,来回答“为什么算法会以周期性的方式运作?”这个问题。
- 第一点:实践中的启发式与信息处理模式
- 核心思想: 周期性是人类和计算机处理信息时的一种自然、方便的“启发式方法”(heuristic)。
- 周期性信息输入: 尽管新闻发布本身非周期性,但很多其他类型的数据馈送天然就是周期性的。
- 价格成交量柱线 (bars): 这是最常见的数据形式,如1分钟K线、5分钟K线。算法基于这些周期性生成的“bars”来做决策。
- 另类数据: 社交媒体帖子、信用卡交易数据等,也常常以固定的时间间隔(如每日、每小时)被打包和更新。[^29]指向了这类数据的例子。
- 周期性预测和执行:
- 算法交易员开发的预测模型(alphas)通常是针对一个“固定期限”的,比如“预测未来10秒的收益率”。
- 基于这个10秒的预测,他们自然会每10秒运行一次模型并执行交易。
- 反证法: “毕竟,很难想象有人会使用 3.1415926 分钟的价格成交量柱线...”。作者用一个生动的例子来说明,使用整数时间间隔(1分钟、5分钟、10秒)是出于便捷、惯例和直观,而非整数间隔则毫无道理。这是一种强大的认知惯性。
- 结论: 算法的周期性行为,是其处理周期性数据和采用周期性决策框架的自然结果,是一种简单有效的实践方式。
- 第二点:与经典均衡模型的联系
- 核心思想: 交易在时间上的“聚集”(clustering),可能是一种市场参与者之间博弈达成的“均衡”状态。
- Admati and Pfleiderer (1991) - Sunshine Trading: 该理论表明,非知情交易者(流动性提供者)为了避免被知情交易者“收割”,会倾向于集中在某个公开的、大家都知道的时间段进行交易(“阳光交易”),从而形成成交量的聚集。知情交易者也喜欢在这种时候交易,因为可以把自己的信息隐藏在巨大的交易量中,降低交易成本。
- Pagano (1989) - Liquidity Clustering: 该理论解释了为什么流动性会倾向于集中在少数几个交易所,因为买家和卖家都想去人最多的地方,以提高成交概率和降低成本。
- 本文的贡献: “我们的发现...意味着交易在时间维度上的集中”。作者将空间维度上的流动性聚集理论,巧妙地拓展到了“时间维度”。整数分钟点就像是时间维度上的“纽交所”,大家(算法)都倾向于在这些“时间热点”进行交易,从而创造出自我实现的流动性和成交量高峰。
- 对知情算法交易员的好处: 在这些周期性的成交量高峰期交易,可以有效降低其大额交易的价格冲击和交易成本。
- 第三点:作为低频行为的高频版本
- 核心思想: 将本文发现的高频周期性,与文献中已知的“低频周期性”联系起来,看作是同一种行为在不同时间尺度上的体现。
- Bogousslavsky (2016): 指出不频繁的再平衡行为(例如,基金经理每天收盘前调仓)会导致收益率和成交量的日度自相关。
- 大量关于基金流的文献: 引用了一系列顶级文献,证明机构投资者的资金流动在日、月、季度频率上存在强烈的规律性模式。例如,共同基金在月末有资金流入/流出的压力,养老金在季末进行资产再平衡等。
- 本文的贡献: “我们的发现可以被视为这些行为的高频版本 (high-frequency version)”。如果说传统机构每季度、每月、每天进行一次“周期性”操作是合理的,那么在算法主导的时代,高频交易员每分钟、每10秒进行一次“周期性”操作,也是完全合乎逻辑的。这为高频周期性的存在提供了深刻的理论和行为金融学上的类比支持。
本段从三个层面为“算法交易为何是周期性的”提供了深刻的解释:1) 从实践操作层面,这是处理周期性数据和采用启发式决策的便捷方式;2) 从市场均衡理论层面,这是交易者在时间维度上自发聚集以寻求流动性和降低成本的结果;3) 从行为金融学层面,这是传统机构低频周期性行为在高频世界中的自然延伸和体现。这三点评论极大地提升了论文的理论深度和解释力。
6行间公式索引
1. 交易量构成关系
2. 周期性强度综合指标 peri 的定义
3. 周期性强度对股票特征的回归模型
4. 日内反转策略的投资组合权重计算
5. 周期性强度对VWAP策略损失及控制变量的回归模型
6. 周期性强度对日内反转策略收益及控制变量的时间序列回归模型
7. 经典的Glosten-Harris价格冲击回归模型
8. 为检验周期性交易而调整后的价格冲击回归模型
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。